Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
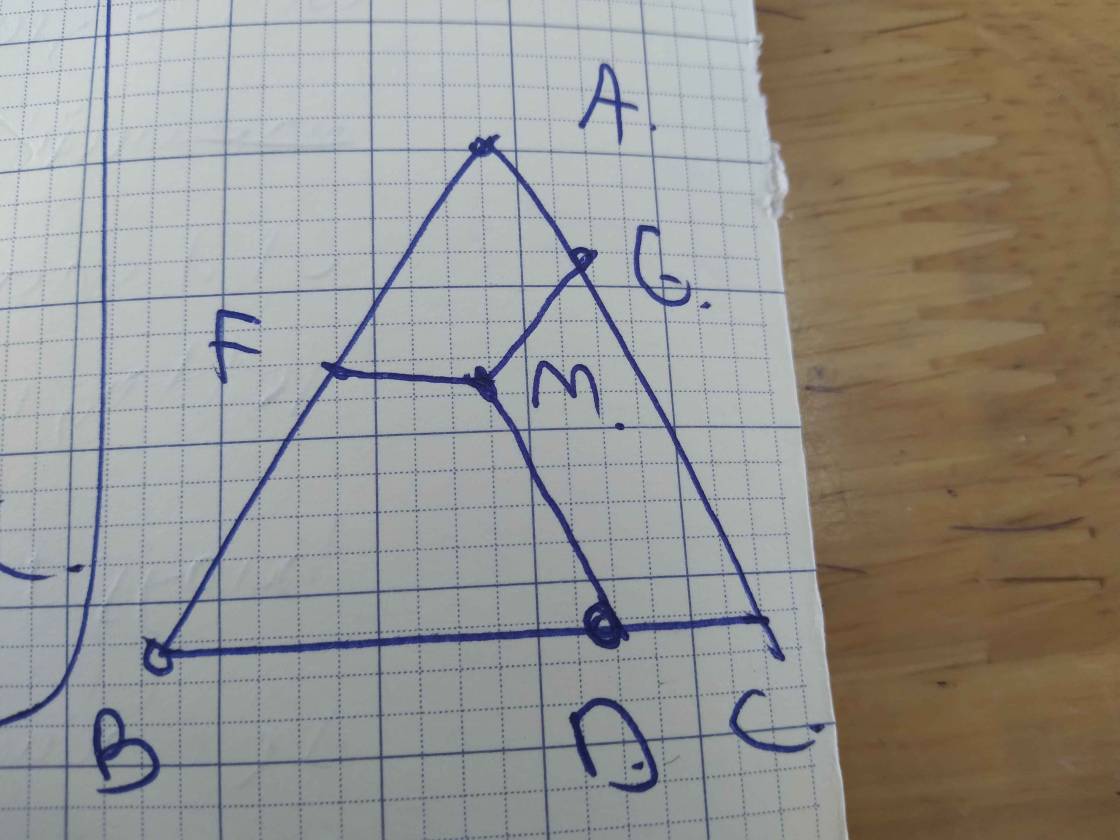
a: HM là đường trung bình của ΔEBC
=>EH=HB
KM là đường trug bình của ΔFBC
=>FK=KC
ΔAHM có EO//HM
=>AE/AH=AO/AM
ΔAKM có KM//FO
nên AF/AK=AO/AM
=>AE/AH=AF/AK
=>EF//HK
b: ΔAHM có EO//HM
=>MA/MO=HA/HE
=>MA/MO=HA/HB
ΔAKM có FO//KM
=>MA/MO=KA/KF=KA/KC
=>HA/HB=KA/KC
=>HK//BC
=>EF//BC

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
=>BH/AB=BC/BA(1)
hay \(AB^2=BH\cdot BC\)
Câu b đề sai rồi bạn

1. △ABI có IL là tia phân giác (gt)
=> \(\dfrac{AI
}{AL}\) = \(\dfrac{BI}{BL}\) <=.> \(\dfrac{AI}{BI}\) = \(\dfrac{AL}{BL}\) (1)
Có AI //MC => △ANI đồng dạng với △CNM
<=> \(\dfrac{AI}{MC}\) = \(\dfrac{AN
}{CN}\) (2)
△ABC có LN // BC (gt)
=> \(\dfrac{AL}{BL}\) = \(\dfrac{AN}{NC}\) (3)
Từ (1), (2), (3) suy ra \(\dfrac{AI}{BI}\) = \(\dfrac{AI
}{MC}\) => BI = MC
Mà BI = IC (vì AI là trung tuyến của tam giác ABC)
nên MC = IC
Do đó △ABC cân tại C
Vì AI // CM => Góc AIN = Góc NMC (so le trong)
Mà góc NMC = góc CIN (vì tam giác MIC cân tại C)
nên Góc AIN = Góc CIN
=> IN là tia phân giác của góc AIC
2. Vì TA//BI (do TD//BC) nên góc ATI = góc TIB (so le trong)
mà góc TIB = góc AIT (vì IL là phân giác)
nên góc ATI = góc AIT => △ATI cân tại A
=> AT = AI (4)
Vì AD//CI (do TD//BC) nên góc ADI = góc DIC (so le trong)
Mà góc DIC = góc AID (vì IN là phân giác góc AIC)
nên góc ADI = góc AID => △ADI cân tại A
=> AD = AI (5)
Ta cộng (4) và (5) thì được AT + AD = 2AI
<=> TD = 2AI

a: Xét ΔABD và ΔEDB có
góc ABD=góc EDB
BD chung
góc ADB=góc EBD
=>ΔABD=ΔEDB
b: Xét tứ giác ABED có
AB//ED
AD//BE
=>ABED là hình bình hành
=>AE cắt BD tại trung điểm của mỗi đường
=>I là trung điểm của AE
=>IA=IE
c: ID=BI
=>ID=1/2BD
=>ID=1/2CD
=>CD=2/3CI
Xét ΔAEC có
CI là trung tuyến
CD=2/3AE
=>D là trọng tâm
mà K là trung điểm của EC
nên A,D,K thẳng hàng