Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Diện tích tam giác ABC ban đầu là
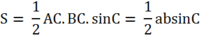
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
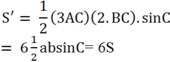

Xét ΔABC có
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{8^2+6^2-AB^2}{2\cdot6\cdot8}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(100-AB^2=48\sqrt{3}\)
=>\(AB=\sqrt{100-48\sqrt{3}}\simeq4,11\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinC\)
\(=\dfrac{1}{2}\cdot6\cdot8\cdot sin30=3\cdot8\cdot\dfrac{1}{2}=3\cdot4=12\)
\(AB=\sqrt{AC^2+BC^2-2.AC.BC.cosC}\)
\(AB=4,11\)
\(S_{ABC}=\dfrac{1}{2}. AC.BC.sinC\)
\(S_{ABC}=\dfrac{1}{2}. 8.6.sin 30^o\)
\(S_{ABC}=12\)

Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
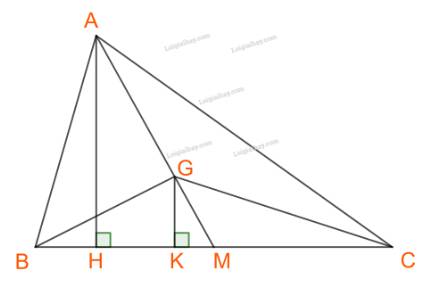
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)

Áp dụng định lý hàm cosin:
\(AC=\sqrt{AB^2+BC^2-2AB.BC.cosB}=\sqrt{2^2+3^2-2.2.3.cos60^0}=\sqrt{2}\)
Diện tích tam giác:
\(S=\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}.2.3.sin60^0=\dfrac{3\sqrt{3}}{2}\)

Kẻ đường cao AH
\(\Rightarrow\Delta AHB\text{ vuông cân tại }H\\ \Rightarrow AH=HB=\cos45^0\cdot AB=\dfrac{\sqrt{2}}{2}\cdot4=2\sqrt{2}\\ \Rightarrow HC=BC-HB=5-2\sqrt{2}\\ \Rightarrow AC=\sqrt{HC^2+AH^2}\approx3,57\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot2\sqrt{2}\cdot5=5\sqrt{2}\left(đvdt\right)\)

\(S_1=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinB\)
\(S_2=\dfrac{1}{2}\cdot3\cdot BC\cdot\dfrac{1}{2}\cdot AB\cdot sinC=\dfrac{3}{4}\cdot BC\cdot AB\cdot sinC\)
=>\(\dfrac{S_2}{S_1}=\dfrac{3}{4}:\dfrac{1}{2}=\dfrac{3}{2}\)
=>Diện tích mới tạo thành bằng 3/2 lần diện tích cũ