

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



gọi K1 là giao điểm của AK với BC. Đầu tiên e chứng minh I là trực tâm của Tam Giác AK1B.
chứng minh tam giác AK1B cân tại K1, rồi suy ra K1M vuông góc vowis AB, suy ra I là trực tâm. rồi e làm như bình thường

Đường thẳng a: 3x - 4y - 31 = 0
Gọi I ( x; y ) là tâm của đương tròn cần tìm
Ta có: d( I; a ) = IA = 5 =>\(\frac{\left|3x-4y-31\right|}{\sqrt{3^2+4^2}}=5\) <=> \(\left|3x-4y-31\right|=25\)<=> 3x - 4y - 31 = 25 ( 1) hoặc 3x - 4y - 31 = -25 ( 2)
a có VTPT \(\overrightarrow{n}\) = ( 3; -4) => a có VTCP \(\overrightarrow{u}\) = ( 4; 3 )
Lại có: IA vuông góc với a => ( 1- x ) . 4 + 3 ( - 7 - y ) = 0 <=> - 4x -3 y = 17 (3)
Từ (1) ; (3) => \(I_1\left(4;-11\right)\)
Từ (2) ; (3) => \(I_2\left(-2;-3\right)\)
Đáp án A

Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.

a)
– Tọa độ trọng tâm G của tam giác ABC là:
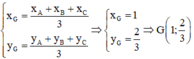
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 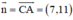 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 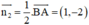 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
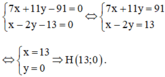
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
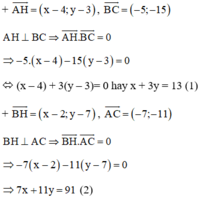
Từ (1) và (2) ta có hệ phương trình
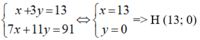
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
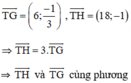
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
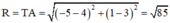
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85

\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất