Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
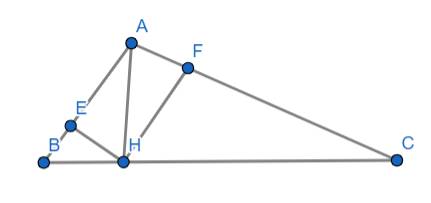
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC

A B C H
Ta có: Tam giác ABC vuông và có góc B bằng 30 độ
=> góc C = 60 độ
=> Tam giác ABC là nửa tam giác đều
=> \(\frac{BC\sqrt{3}}{2}=AB=5\left(cm\right)\)
=> BC= \(\frac{5.2}{\sqrt{3}}=\frac{10}{\sqrt{3}}\)
=> AC = \(\frac{10}{\sqrt{3}}:2=\frac{5\sqrt{3}}{3}\) (cm)
=> AH = \(\frac{AB.AC}{BC}=\frac{5}{2}\left(cm\right)\)
b, Stam giác ABC=\(\frac{AB.AC}{2}=\frac{25\sqrt{3}}{6}\left(cm^2\right)\)
a, Vì \(BC^2=AB^2+AC^2\) nên tg ABC vuông tại A
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\)
b, \(S_{ABC}=\dfrac{1}{2}AB\cdot AC=30\left(cm^2\right)\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
=>AH=60/13(cm)