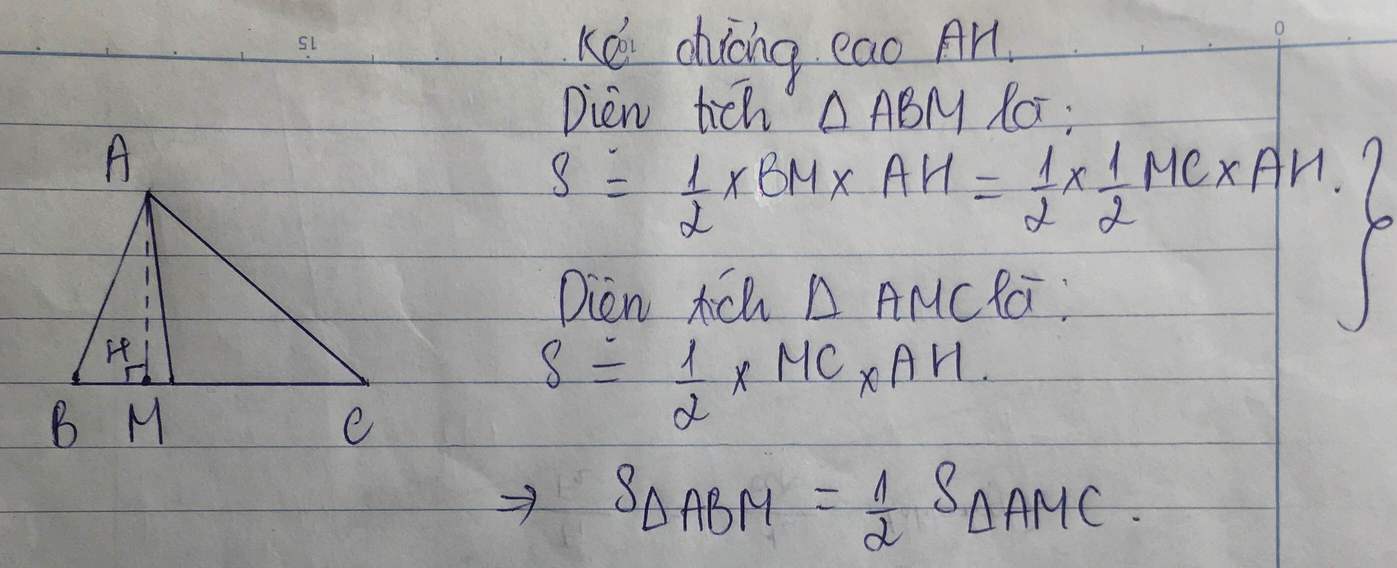Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

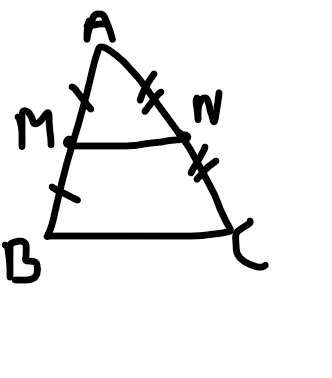
Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90

a,có:S AMN =1/2 S ABC
=>S ABC = 2.5 AMN = 2.3=6 cm2
b,có 2.MN=BC
=>MN=BC/2 = 6/2 = 3 cm


Xét hai tam giác EAN và ENC ta thấy chúng có chung đường cao từ E xuống AC và CN=3AN =>S(CNE)=3S(ENA).
Lại có S(EBM)=S(EMC) Do có chung đường có hạ từ E xuống BC và BM=CM
tương tự có :S(NBm) =S (M NC) =>S (BNE) =S(NEC) = 27 x3 = 81 => S(BAN) = 81-27 = 54
Để ý thấy: S(BNC) = 3 S( BNA) Vì có chung đường cao Kẻ tu B va CN = 3 NA =.S(ABC)=S(ABN) x4 = 54 x4 =216

Xét hai tam giác EAN và ENC ta thấy chúng có chung đường cao từ E xuống AC và CN=3AN =>S(CNE)=3S(ENA).
Lại có S(EBM)=S(EMC) Do có chung đường có hạ từ E xuống BC và BM=CM
tương tự có :S(NBm) =S (M NC) =>S (BNE) =S(NEC) = 27 x3 = 81 => S(BAN) = 81-27 = 54
Để ý thấy: S(BNC) = 3 S( BNA) Vì có chung đường cao Kẻ tu B va CN = 3 NA =.S(ABC)=S(ABN) x4 = 54 x4 =216

Nối EC ; NB ta có:\(S\left(EBM\right)=S\left(EMC\right);S\left(NBM\right)=S\left(NMC\right)\)
\(\Rightarrow S\left(NBE\right)=S\left(NEC\right)\)
Mặt khác : \(S\left(NCE\right)=S\left(NEA\right).3=81\left(cm^2\right)\)
\(S\left(ABN\right)=81-26=54\left(cm^2\right)\)
Khi đs : \(S\left(ABN\right)=\frac{1}{4}.S\left(SBC\right)\Rightarrow S\left(ABC\right)=54:\frac{1}{4}=216\left(cm^2\right)\)