NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2021
Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\
=\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\
=\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)
4 tháng 2 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7.2\left(cm\right)\)
c: CH=BC-BH=20-7,2=12,8(cm)
Xét ΔACH vuông tại H có \(\sin C=\dfrac{AH}{AC}=\dfrac{9.6}{16}=\dfrac{3}{5}\)
nên \(\widehat{C}=37^0\)
=>\(\widehat{CAH}=53^0\)
d: XétΔABC có AD là đường phân giác
nên BD/AB=CD/AC
=>BD/12=CD/16
hay BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
Do đó: BD=60/7(cm); CD=80/7(cm)
14 tháng 7 2021
Áp dụng hệ quả của định lý Cosin ta có:
\(\cos C=\dfrac{b^2+a^2-c^2}{2ab};\cos B=\dfrac{c^2+a^2-b^2}{2ca}\)
\(\Rightarrow b\cos C+c\cos B=b\dfrac{b^2+a^2-c^2}{2ab}+c\dfrac{c^2+a^2-b^2}{2ca}=\)
\(\dfrac{b^2+a^2-c^2}{2a}+\dfrac{c^2+a^2-b^2}{2a}=\dfrac{2a^2}{2a}=a\)
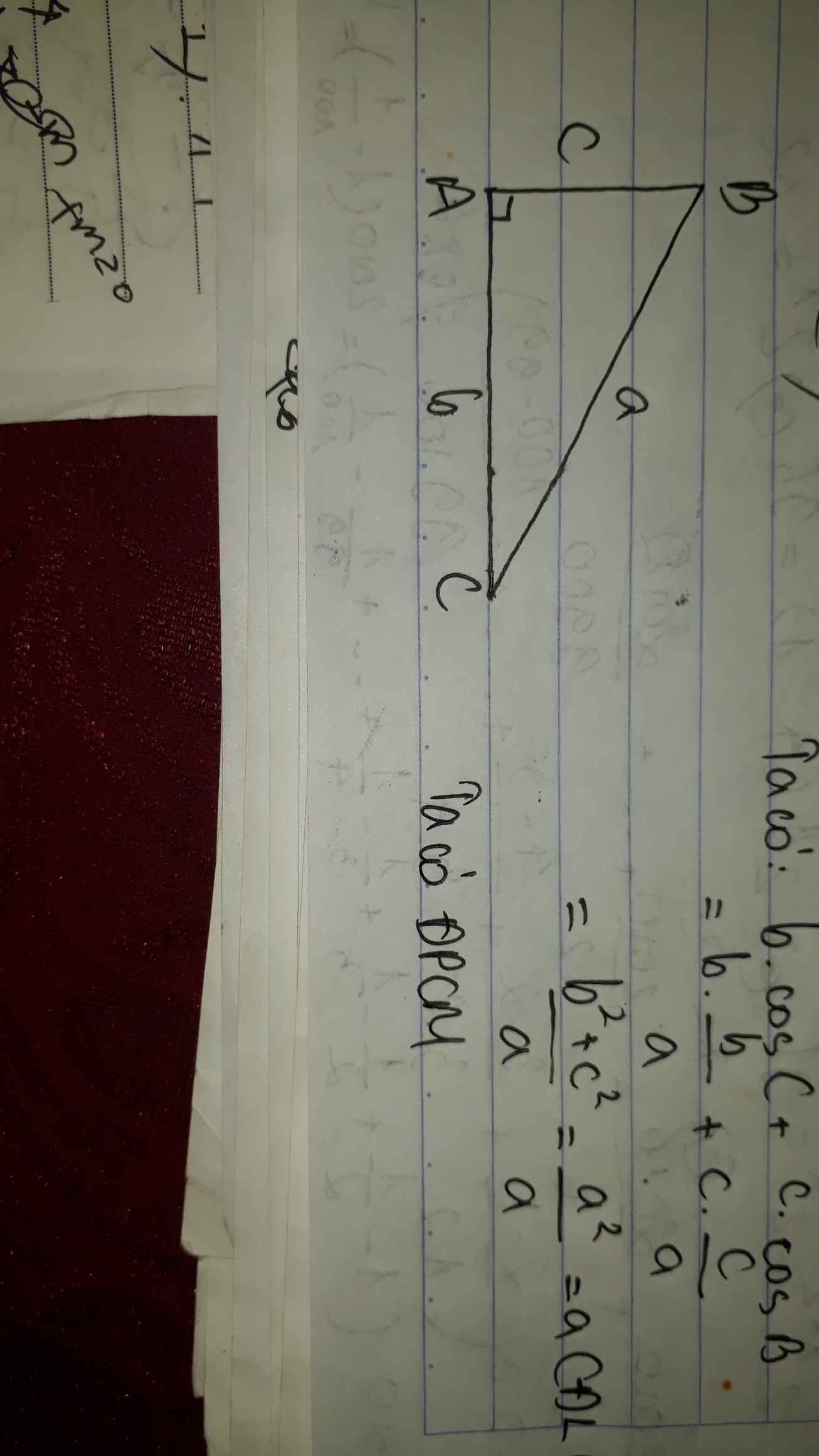
ta có cos b =ab/bc
<=> abc vuông
nói nôm na là cos b = kề/huyền
chỉ có tam giác vuông mới có cạnh huyền => tam giác abc vuông