K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên


Giải:
Bạn tự vẽ hình nhé!
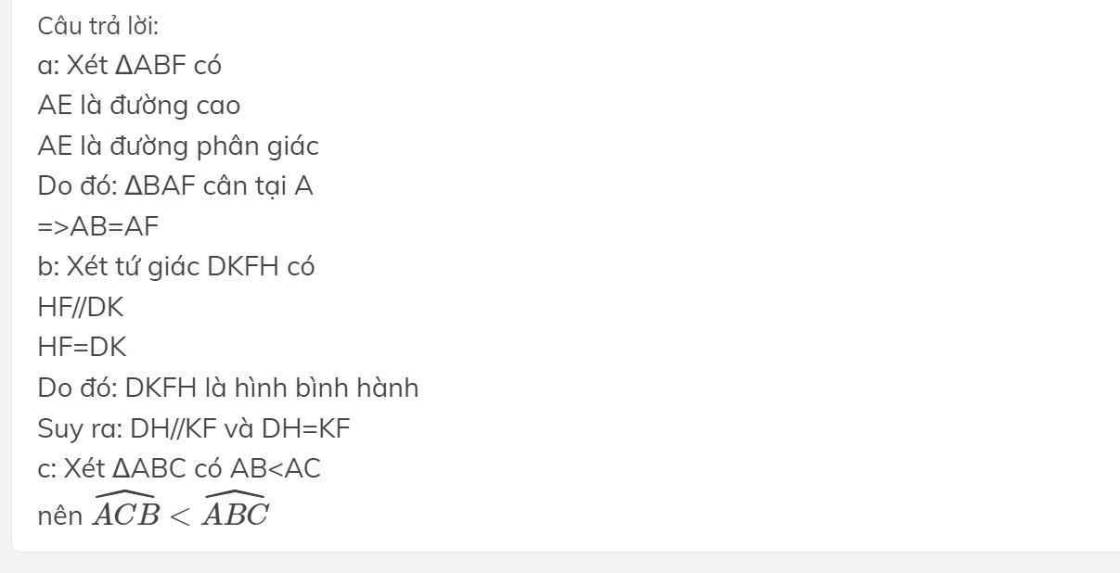
a, Vì AD là tia phân giác của \(\widehat{BAC}\) (gt)
nên \(\widehat{BAD}=\widehat{CAD}\)
hay \(\widehat{EAF}=\widehat{BAE}\), \(\widehat{BAD}=\widehat{DAF}\)
Mà BE _|_ AD tại E (gt)
\(\Rightarrow\widehat{AEB}=\widehat{AEF}=90^o\)
Xét \(\Delta ABE\) và \(\Delta AEF\) có:
\(\hept{\begin{cases}\widehat{AEB}=\widehat{AEF}\left(cmt\right)\\ADchung\\\widehat{BAE}=\widehat{EAF}\left(cmt\right)\end{cases}}\Rightarrow\Delta ABE=\Delta AFE\left(g.c.g\right)\)
\(\Rightarrow AB=AF\) (2 cạnh tương ứng) (đpcm)
b, Vì FH // BC (gt)
nên FH // DK
\(\Rightarrow\widehat{DFH}=\widehat{FDK}\) (2 góc so le trong)
\(\widehat{FHK}=\widehat{DKH}\) (2 góc so le trong)
Xét \(\Delta DFH\) và \(\Delta DFK\) có:
\(\hept{\begin{cases}FH=DK\left(gt\right)\\\widehat{DFH}=\widehat{FDK}\left(cmt\right)\\DFchung\end{cases}}\Rightarrow\Delta DFH=\Delta FDK\left(g.c.g\right)\)
\(\Rightarrow DH=FK\) (2 cạnh tương ứng) (1)
\(\widehat{DFK}=\widehat{FDH}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow FK//DH\) (dấu hiệu nhận biết) (2)
Từ (1), (2) ta có đpcm
c, Xét \(\Delta ABD\) và \(\Delta ADF\) có:
\(\hept{\begin{cases}ADchung\\\widehat{BAD}=\widehat{DAF}\left(cmt\right)\\AB=AF\left(cmt\right)\end{cases}}\Rightarrow\Delta ABD=\Delta AFD\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{AFD}\) (2 góc tương ứng) (3)
Ta có: \(\widehat{AFD}\) là góc ngoài của \(\Delta CDF\) tại đỉnh F
\(\Rightarrow\widehat{AFD}>\widehat{C}\) (4)
Từ (3), (4)
\(\Rightarrow\widehat{ABD}>\widehat{C}\)
hay \(\widehat{ABC}>\widehat{C}\) (đpcm)