Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, từ E hạ I,K xuống AB,BC.
=>EI=EK (vì BE là phân giác g.ABC).
=>ΔAIE = ΔCKE. (cạnh huyên - cạnh góc vuông).
=>gIAE = gECK.
=>tứ giác AECB nt.
vì gBAC=90 độ nên góc này chắn đường kính.=>BC là đường kính.
=>tâm O là trung điểm của BC.
2, có AC=căn(50^2 - 14^2)=48.
EK=EI=AC/2=24.
có EK/EB = sinEBC=sin(ABC/2).
có cosABC=14/50 nên sin(ABC/2)=3/5 (tính nhờ công thức cos2a=1-2(sinx)^2 ).
=>EB = 24/(3/5)=40.
3, gọi H là giao điểm của AF và BE.
gEBF=gFAE=90độ.
=>FA,EB là 2 đường cao của ΔPEF. => PH vg EF.(1)
vì AB // EF nên AEFB là hình thang cân.=>gAEF=gBFE.
=>ΔPEF cân ở P.=>PO vừa là trung tuyến vừa là đường cao.
=>PO vg EF. (2)
từ (1) và (2)=>P,H,O thẳng hàng.
4, tính S hình tròn (O): S=πR^2=π.25^2=625π.
tính S ngũ giác: S(ABFCE)=S(ABF) + 2S(AFE)=(1/2).(AC/2).AB + 2.(1/2).(AC/2).EF.
=1368.
=> S phần hình tròn nằm ngoài ABFCE là 625π - 1368.

Xét tam giác ABC
có ^A+^B+^C=180
Thay 60+^b+50=180
=>^B=180-60-50=70 độ
Xét tam giác ABD có
^A+^D+^B=180
THAY 60+d+70:2=180
=>d= 85
tìm cdb tương tự

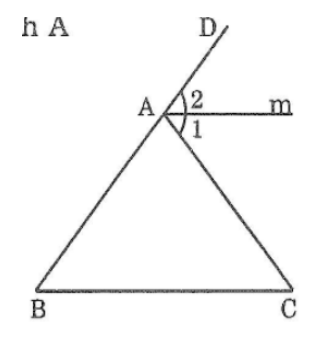
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A
⇒∠(CAD ) =∠B +∠C =50o+50o=100o
(tính chất góc ngoài tam giác)
∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50o (vì tia Am là tia phân giác của ∠(CAD)
Suy ra: ∠(A1) =∠C =50o
⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

1) đề thiếu nhé
2) Sửa lại : AM | BC
+) Góc A + B + C = 180o => A + 50o + 50o = 180o => A = 80o
=> góc BAM = A/2 = 40o
+) Tam giác BAM có: góc BAM + B + AMB = 180o => 40o + 50o + AMB = 180o => AMB = 90o
=> AM | BC

A B C M 1 2 Q G
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)

Gọi góc ngoài đỉnh A chứa tia phân giác Am là \(\widehat{xAB}\)
Xét tam giác ABC có \(\widehat{xAB}\) là góc ngoài => \(\widehat{xAB}=\widehat{ABC}+\widehat{ACB}=50^0+50^0\)\(=100^0\)
Vì Am là tia phân giác \(\widehat{xAB}\)=> \(\widehat{xAm}=\widehat{mAB}=\frac{\widehat{xAB}}{2}=\frac{100^0}{2}=50^0\)
Ta thấy \(\widehat{mAB}=\widehat{ABC}\left(=50^0\right)\)mà chúng là 2 góc so le trong
=> Am // BC (đpcm)
xét tam giác ABM và tam giác ACM có:
A1=A2 (GIẢ THUYẾT)
AM:cạnh chung
GÓC B=GÓC C(=50\(^O\))
DO đó tam giác ABM = tam giác ACM(G.C.G)

Bài 1:
A B C E 50
a) Vì AE // BC nên góc AEB = EBC ( so le trong ) (1)
mà góc ABE = EBC ( BE là tia phân giác của góc ABC ) (2)
nên từ (1) và (2) suy ra góc AEB = ABE
mà 2 góc này là 2 góc đáy
=> ΔABE là tam giác cân
b) Do góc ABE = EBC = 50:2 = 25 độ
nên góc ABE = AEB = 25 độ
Ta có: ABE + AEB + BAE = 180 độ ( tc tổng 3 góc trong 1 tg )
=> 25 + 25 + BAE = 180
=> BAE = 130 độ.
Bài 2:
A B C D E
a) Vì ΔABC cân tại A nên góc ABC = ACB
mà góc ABC + ACB = 180 - BAC
=> góc ABC = 180 - BAC /2 (1)
Do AD = AE nên ΔADE cân tại A
được góc ADE = AED
mà góc ADE + AED = 180 - BAC
=> ADE = 180 - BAC/2 (2)
Từ (1) và (2) suy ra góc ABC = ADE
mà 2 góc này ở vị trí đồng vị => DE//BC
b) Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE ( gt); AB = AC (theo câu a)
=> DB = EC
Xét ΔMBD và ΔMCE có:
DB = CE ( chứng minh trên )
Góc ABC = ACB ( theo câu a )
MB = MC ( suy từ gt)
=> ΔMBD = ΔMCE ( c.g.c )
c) Lại do ΔMBD = ΔMCE (theo câu b)
=> MD = ME (2 cạnh tương ứng)
Xét ΔAMD và ΔAME có:
AD = AE (gt)
AM chung
MD = ME ( cm trên )
=> ΔAMD = ΔAME ( c.c.c )
Chúc bạn học tốtNgân Phùng![]()
Sửa lại bài 3:
x A B C m 1
Giải:
Vì tam giác ABC cân tại A nên \(\widehat{B}=\widehat{C}\)
Xét góc ngoài \(\widehat{xAC}=\widehat{B}+\widehat{C}\)
\(\Rightarrow\frac{1}{2}\widehat{xAC}=\widehat{C}\)
\(\Rightarrow\widehat{A_1}=\widehat{C}\)
Mà 2 góc trên ở vị trí so le trong nên Am // BC
Vậy Am // BC
trong tam giác ABC có:
A+B+C=1800
A+1000 =1800 \(\Rightarrow\widehat{A}\)=800
\(\Rightarrow\)góc ngoài tại đỉnh A =1800 -800 =1000
Mặt khác: Am là p/g góc ngoài tại đỉnh A => \(\widehat{CAm}=\widehat{mAn}\)=1000 :2=500 (n là cái tia ở trên,mk đặt z)
=>\(\widehat{CAm}=\widehat{B}=50^0\)Mà \(\widehat{CAm}\)và \(\widehat{B}\) là 2 góc so le trong
Vậy Am // BC
chắc là z mk ngu hình