Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

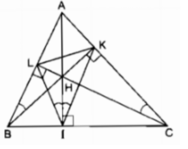
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.


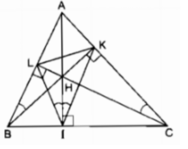
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác BIHL nội tiếp.

Tứ giác CIHK nội tiếp.

Từ (1), (2) suy ra:
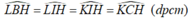

a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành

a: A,E,D,B cùng thuộc (O)
=>AEDB nội tiếp
A,E,C,B cùng thuộc (O)
=>AECB nội tiếp
B,E,C,D cùng thuộc (O)
=>BECD nội tiếp
góc AHB=góc AKB=90 độ
=>AKHB nội tiếp
b: Đề sai rồi bạn


Bài 1:
b)
chứng minh EDCB là tgnt => góc AED = góc ACB
từ đó, chứng minh tam giác AED đồng dạng ACB (gg)
=> DE / BC = AD / AB
tam giác ADB vuông tại A => AD / AB = cotg A = cotg 45 = 1
c)
kẻ tiếp tuyến tại Ax của (O) (Ax thuộc nửa mp bờ AC chứa B)
góc xAB = ACB = AED
=> DE // Ax
Mà Ax vuông góc với OA nên OA vuông góc với DE. (đpcm)

Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có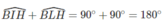
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có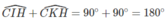
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có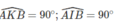
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có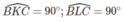
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có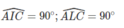
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.