Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI

a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI

Giải thích các bước giải:
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH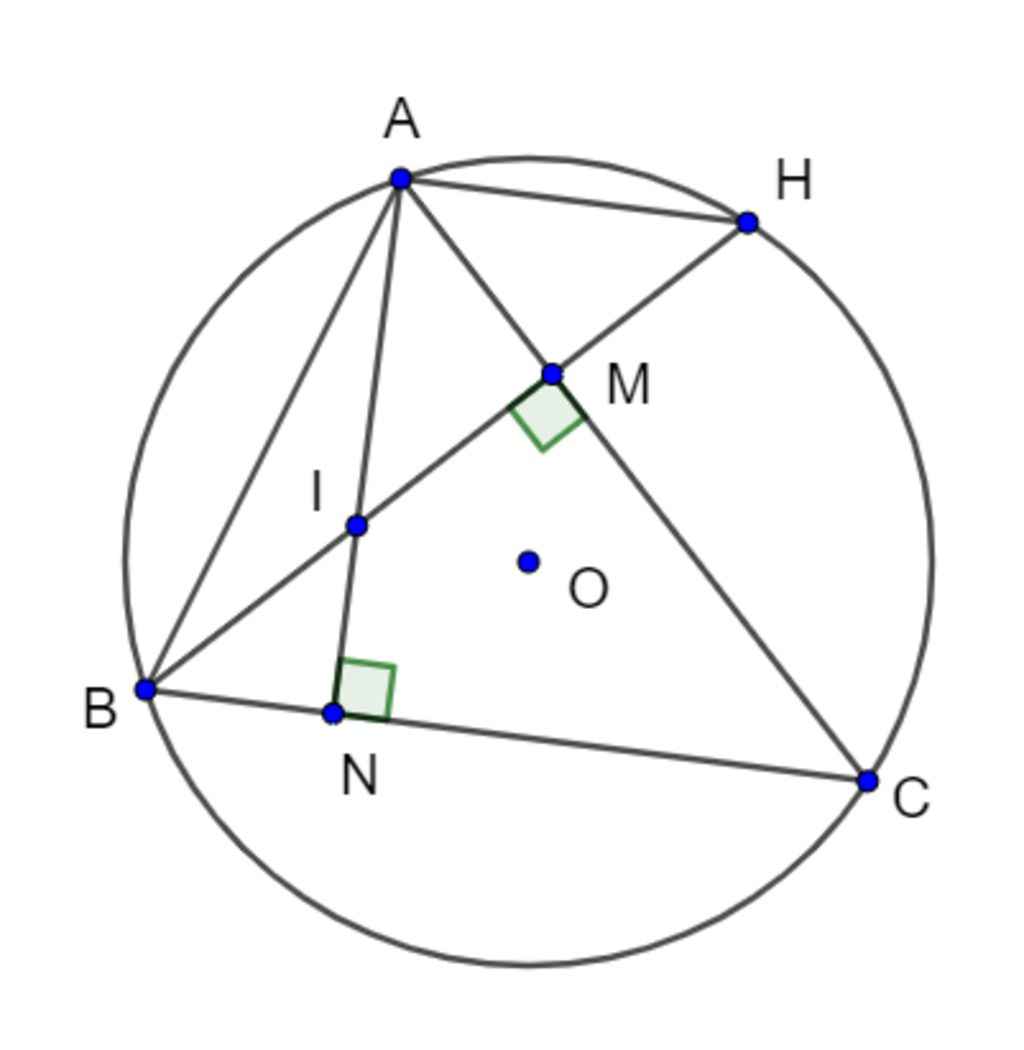

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

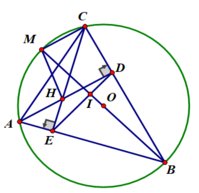
c) Do tứ giác AEDC là tứ giác nội tiếp nên ∠(CAB) = ∠(IDB) (cùng bù ∠(CDE) )
Mặt khác ∠(CAB) = ∠(CMB) (2 góc nội tiếp cùng chắn cung BC)
⇒ ∠(CMB) = ∠(IDB)
⇒ Tứ giác CMID là tứ giác nội tiếp ( Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)

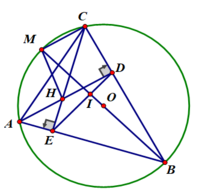
a) Xét tứ giác AEDC có:
∠(AEC) = ∠(ADC) = 90 0
Mà 2 góc này cùng nhìn cạnh AC
⇒ Tứ giác AEDC là tứ giác nội tiếp
a: góc INC+góc IMC=180 độ
=>INCM nội tiếp
b: Xét ΔINB vuông tại N và ΔIMA vuông tại M có
góc NIB=góc MIA
=>ΔINB đồng dạng với ΔIMA
=>IN/IM=IB/IA
=>IN*IA=IM*IB
c: góc AIH=góc BIN=góc BCA
=>góc AIH=góc AHI
=>AI=AH