Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, HS tự chứng minh
b, HS tự chứng minh
c, HS tự chứng minh
d, ∆MIH:∆MAB
=> M H M B = I H A B = 2 E H 2 F B = E H F B
=> ∆MHE:∆MBF
=> M F A ^ = M E K ^ (cùng bù với hai góc bằng nhau)
=> KMEF nội tiếp => M E F ^ = 90 0

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

Giải chi tiết:
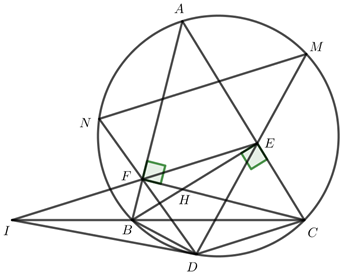
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

a: góc BIM=góc BHM=90 độ
=>BMHI nội tiếp
b: góc CBM=góc MAC=góc MAK
=>góc MAK=góc MIK
1/Xét tứ giác MIHC có:
góc MIC=90 độ (MI vuông góc với AC tại I)(1)
góc MHC=90 độ (MH vuông góc với BC tại H)(2)
Từ (1) và (2)=> tứ giác MIHC nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc 90 độ)
=> góc IHM=góc ICM (cùng chắn cung IM)(đpcm)
2/Tứ giác ABCM nội tiếp (O)
=> góc MCB= góc MAK (3)
Tứ giác MIHC nội tiếp (c/m trên)
=>góc MCB= góc MIK (4)
Từ (3) và (4)=> góc MAK= góc MIK
=> Tứ giác AIMK nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới 1 góc an-pha)
=>góc AKM+góc AIM=180 độ
=>góc AKM=90 độ (vì góc AIM= 90 độ)
=>MK vuông góc với BK tại K( đpcm)
Còn câu 3 và 4 đề ko có D và F nên mk ko c/m dc
chị ơi! cái này em chưa học nên chưa biết trả lời lời làm sao mong chị thông cảm