Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

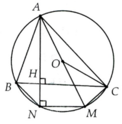
a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân

a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
hay \(\widehat{ACM}=90^0\)
b: \(\widehat{OAC}+\widehat{AMC}=90^0\)
\(\widehat{BAH}+\widehat{ABC}=90^0\)
mà \(\widehat{AMC}=\widehat{ABC}\)
nên \(\widehat{OAC}=\widehat{BAH}=\widehat{OCA}\)
Xét \(\Delta OAC\) có : \(OA=OC\left(=R\right)\left(gt\right)\)
\(\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OAC}=\widehat{ACO\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow\widehat{BAH=\widehat{OCA}}\)
c) Xét \(\left(O\right)\), có : \(\widehat{ANM=90^0}\)
\(\Rightarrow MN\pm AN\)
\(MàBC\pm AN\left(gt\right)\)
\(\Rightarrow MN=BC\)
Xét tam giác \(BNMC\)\(cóMN=BC\left(cmt\right)\)
Tam giác BNMC là hình thang
Mà bốn đỉnh B,M,N,C
Vậy BMNC là tam giác cân

\(a,\widehat{ACM}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(b,\widehat{ABC}=\widehat{AMC}=\dfrac{1}{2}sđ\mathop{AC}\limits^{\displaystyle\frown}\)
Mà \(\widehat{ABH}+\widehat{ABC}=\widehat{OAC}+\widehat{AMC}=90^0\)
Do đó \(\widehat{ABH}=\widehat{OAC}\)
\(c,\widehat{ANM}=90^0\) (góc nội tiếp chắn nửa đường tròn)
Do đó \(MN\bot AN\)
Mà \(BC\bot AN \Rightarrow BC//MN\)
Do đó BCMN là hình thang
Mà \(B,M,N,C\in (O)\)
Vậy BCMN là hình thang cân

a)Gọi I là trung điểm của tam giác BC
Áp dụng đường trung tuyến cạnh huyền của tam giác EBC và DBC
=>IE=ID=IB=IC
=> tứ giác BCDE nội tiếp. tâm đường tròn là I
b)AFK=90 ( dg cao thứ 3)
ACK=90 (chắn nữa dg tròn)
=>AFB=ACK
c)BD vg góc với AC
ACK=90 =>CK vg góc với AC
=>CK song song với BH
tuong tu CH song song voi BK
=>BHCK là hinh binh hanh
*vì I là trung điểm của BC
=>I cung la trung diem cua HK
=>H,I,K thang hang
a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
b: \(\widehat{BAH}+\widehat{ABC}=90^0\)
\(\widehat{OAC}+\widehat{AMC}=90^0\)
mà \(\widehat{ABC}=\widehat{AMC}\left(=\dfrac{sđ\stackrel\frown{AC}}{2}\right)\)
nên \(\widehat{BAH}=\widehat{OAC}=\widehat{OCA}\)
Bạn chưa tính góc AMC kìa :))))