Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi K là trung điểm của BE
Ta có KM là đg trung bình của tam giác BEC
\(KM=\frac{1}{2}EC\)(1)
và KM//AC
Suy ra: góc KMD=DAE(slt)
Chứng minh tam giác ADE=tam giác MDK
Suy ra: \(AE=KM\)(2)
Từ (1) và (2)
Vậy.....

a: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{BM}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\left(1\right)\)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
c: Xét ΔABC có
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC

Lời giải:
Áp dụng định lý Menelaus cho tam giác $AMC$ có $B,D,E$ thẳng hàng:
$\frac{BM}{BC}.\frac{DA}{DM}.\frac{EC}{EA}=1$
$\Leftrightarrow \frac{1}{2}.1.\frac{EC}{EA}=1$
$\Leftrightarrow EC=2EA$ hay $EA=\frac{1}{2}EC$ (đpcm)

Xét ΔBEC có
M là trung điểm của BC
F là trung điểm của EC
Do đó: MF là đường trung bình của ΔBEC
Suy ra: MF//DE
Xét ΔAMF có
D là trung điểm của AM
DE//MF
Do đó: E là trung điểm của AF
Suy ra: AE=EF
mà EF=FC
nên AE=FE=FC
hay \(AE=\dfrac{EC}{2}\)

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
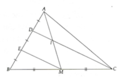
ko biết làm
vc bạn tôi