Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giác ABC vuông tại A,có ABcho tam giác ABC vuông tại A,có AB<AC.Gọi M và n lần lượt là hình chiếu của D trên AB và AC,BN cắt CM tại K,AK cắt Dm tại I,BN cắt DM tại E ,CM cắt DN tại F.a) chứng minh EF song song BC b) C/m K là trực tâm tam giác AEFc) tính góc BID
ĐS: chiu thúa

a. -Xét △ABC: AD là đường phân giác (gt)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (định lí về đường phân giác trong tam giác)
\(\Rightarrow\dfrac{AB}{16}=\dfrac{6}{8}\)
\(\Rightarrow AB=\dfrac{6}{8}.16=12\left(cm\right)\)
b) -Xét △ABC: DE//AB (gt)
\(\Rightarrow\dfrac{EA}{EC}=\dfrac{BD}{CD}\) (định lí Ta-let)
Mà \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(cmt\right)\)
\(\Rightarrow\dfrac{EA}{EC}=\dfrac{AB}{AC}\) nên \(AC.EA=AB.EC\)
c) -Ta có: \(\widehat{BAD}=\widehat{CAD}\) (AD là tia phân giác của \(\widehat{BAC}\))
Mà \(\widehat{BAD}=\widehat{ADE}\) (AB//DE và so le trong)
\(\Rightarrow\widehat{CAD}=\widehat{ADE}\) nên △ADE cân tại E.
\(\Rightarrow AE=DE\)
-Xét △AIE: AP là đường phân giác.
\(\Rightarrow\dfrac{PE}{PI}=\dfrac{AE}{AI}\)(định lí về đường phân giác trong tam giác)
Mà \(AE=DE\left(cmt\right)\); \(AI=BI\) (I là trung điểm AB)
\(\Rightarrow\dfrac{PE}{PI}=\dfrac{DE}{BI}\)
-Xét △QDE: DE//BI.
\(\Rightarrow\dfrac{QD}{QI}=\dfrac{DE}{BI}\) (hệ quả định lí Ta-let)
Mà \(\dfrac{PE}{PI}=\dfrac{DE}{BI}\) nên \(\dfrac{PE}{PI}=\dfrac{QD}{QI}\)

a/ Xét tg DIE và tg CID có
\(\widehat{CDE}=\widehat{BCD}\) (góc so le trong)
\(\widehat{BED}=\widehat{CBE}\) (góc so le trong)
=> tg DIE đồng dạng tg CID (g.g.g)
b/
Ta có DE//BC
Xét tg ABM có \(\dfrac{DN}{BM}=\dfrac{AN}{AM}\) (1)
Xét tg ACM có \(\dfrac{EN}{CM}=\dfrac{AN}{AM}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{DN}{BM}=\dfrac{EN}{CM}\) mà BM=CM => DN=EN
c/
Nôi A với I cắt DE tại N'; cắt BC tại M'
Ta có
\(\dfrac{DN'}{CM'}=\dfrac{IN'}{IM'}\)
\(\dfrac{EN'}{BM'}=\dfrac{IN'}{IM'}\)
\(\Rightarrow\dfrac{DN'}{CM'}=\dfrac{EN'}{BM'}\) (1)
Ta có
\(\dfrac{EN'}{CM'}=\dfrac{AI}{AM'}\)
\(\dfrac{DN'}{BM'}=\dfrac{AI}{AM'}\)
\(\Rightarrow\dfrac{EN'}{CM'}=\dfrac{DN'}{BM'}\) (2)
Công 2 vế của (1) và (2)
\(\dfrac{DN'+EN'}{CM'}=\dfrac{EN'+DN'}{BM'}\Rightarrow\dfrac{DE}{CM'}=\dfrac{DE}{BM'}\)
=> CM' = BM' => M' là trung điểm của BC => M trùng M'
Từ (1) => DN'=EN' => N' là trung điểm của DE mà N là trung điểm của DE => N trùng N'
=> N; I; M thẳng hàng

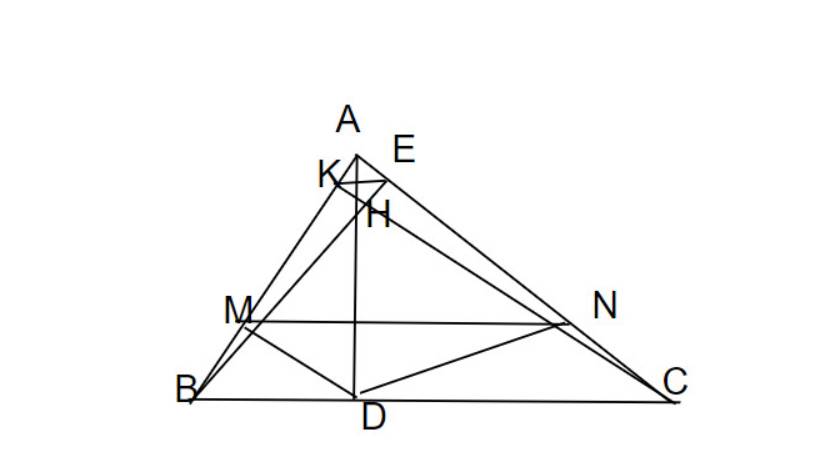
xét ΔAKH và Δ AMD, có
\(\widehat{A}=\widehat{A}\\ \widehat{K}=\widehat{M}=90^o\\ \Rightarrow\text{ }\Delta AKH\sim\Delta AMD\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AH}{AD}=\dfrac{AK}{AM}\)(1)
xét ΔAKE và Δ AMN, có:
\(\widehat{A}\) chung
\(\widehat{E}=\widehat{N}\) đồng vị
\(\Rightarrow\text{ }\Delta AKE\sim\Delta AMN\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AE}{AN}=\dfrac{AK}{AD}\)(2)
xét ΔAHE và Δ ADN, có:
\(\widehat{A}\) chung
từ (1) và (2) ta suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AN}\\ \Rightarrow\Delta AHE~\Delta ADN\)
\(\Leftrightarrow\widehat{E}=\widehat{N}=90^o\Rightarrow DN\perp AC\left(đpcm\right)\)
P/S: chúc bạn học tốt nhe, mình vẽ hình xong nhìn muốn nội thương=))