Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình như trên
+)Ta có: ΔDMB=ΔENCΔDMB=ΔENC ( g-c-g) ( Vì ˆMBD=ˆNCEMBD^=NCE^ cùng bằng ˆACBACB^)
Nên MD = NE.
+)Xét ΔDMIΔDMI và ΔENIΔENI: ˆD=ˆE=900,MD=NE(cmt)D^=E^=900,MD=NE(cmt)
ˆMID=ˆNIEMID^=NIE^( Hai góc đối đỉnh)
Nên ΔDMI=ΔENIΔDMI=ΔENI( cgv - gn)
⇒MI=

a, Theo định lý Py-ta-go ta có:
AB2 + AC2 = BC2
62 +82 = BC2
Suy ra : BC2 = 82 + 62 =100
BC = 10 cm
b, Xét tam giác DAB và tam giác DEB ta có :
- B1=B2 (gt)
- BD là cạnh chung
- BE=BA (gt)
Suy ra tam giác DAB= DEB ( C.G.C)
Vậy : AD=AE (hai góc tương ứng )
Góc DAB= Góc DEB = 90 độ (hai góc tương ưng)
Hay DE vuông góc với BC
a/xét tg ABC vuông tại A :\(BC^2=AB^2+AC^2\\ BC^2=6^2+8^2\\ BC^2=36+64=100\\ BC=\sqrt{100}\\ BC=10\)
b/ xét tg ABD và tg BED :
BA = BE (gt)
BD cạnh chung
góc ABD = góc EBD (gt)
vậy tg ABD = tg EBD (c.g.c)
=> AD = ED (ctứ)
DE vg BE '' ko bít làm '' tớ hc ko giỏi ''

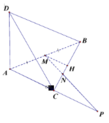
Chọn hệ trục tọa độ Oxyz. Có O = A, AB = Ox, AC = Oy, AD = Oz, AD = 2 α tan 60 o = 2 a 3 , N H = 1 2 - 1 3 B C = 1 6 B C = 1 2 N C
Từ M kẻ MH song song với AC ta có MH = a; CP = 2MH = 2a ⇒ AP = 4a
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1 . Vậy khoảng cách từ P ( 0;4a;0 ) đến (BCD) là:
1 1 4 a 2 + 1 4 a 2 + 1 12 a 2 = a 12 7 = 2 a 21 7
Đáp án cần chọn là A

a) Thấy 52=32+42 hay BC2=AB2+AC2
\(\Rightarrow\Delta ABC\) vuông tại A
b)Hình thì chắc bạn tự vẽ được nha![]()
![]()
![]()
Xét 2\(\Delta ABH\) và\(\Delta DBH\) có:
AB=DB
\(\widehat{BAH}=\widehat{BDH}\)
BH chung
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\)
\(\Rightarrow\)BH là tia phân giác \(\widehat{ABC}\)
c)tam giác ABC đã có các cạnh có độ dài khác nhau nên tam giác ABC ko cân được đâu chị
a) Ta có :
-BC2=52=25(1)
-AB2+AC2=32+42=25(2)
-Từ (1)và(2)suy ra BC2=AB2+AC2
-do đó tam giác ABC vuông tại A(áp dụng định lý Py-ta-go đảo)
-vậy tam giác ABC là tam giác vuông .
b)Xét \(\Delta\) ABH(vuông tại A) và \(\Delta\) DBH(vuông tại D) có
-BH là cạnh huyền chung
-AB=BD(gt)
-Do đó:\(\Delta\) ABH=\(\Delta\) DBH(cạnh huyền-cạnh góc vuông)
\(\Rightarrow\)Góc ABH =Góc DBH(hai góc tương ứng)
Vậy BH là tia phân giác của góc ABC

C/m 3 điểm thẳng hàng là tìm trọng tâm của tam giác đóa pạn, có trọng tâm ròi =>D,M.F thẳng hàng