Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{C}=30^0\)
\(\widehat{ABI}=\widehat{CBI}=30^0\)
b: Xét ΔBAI và ΔBDI có
BA=BD
\(\widehat{ABI}=\widehat{DBI}\)
BI chung
Do đó: ΔBAI=ΔBDI
Suy ra: \(\widehat{BAI}=\widehat{BDI}=90^0\)
hay DI⊥BC
c: Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)
nên ΔIBC cân tại I
mà ID là đường cao
nên D là trung điểm của BC
d: Xét ΔAIK vuông tại A và ΔDIC vuông tại D có
IA=ID
\(\widehat{AIK}=\widehat{DIC}\)
Do đó: ΔAIK=ΔDIC
Suy ra: IK=IC
hay ΔIKC cân tại I
e: Xét ΔBKC có BA/AK=BD/DC
nên AD//KC

a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: góc MAD+góc BAD=90 độ
góc DAH+góc BDA=90độ
góc BAD=góc BDA
=>góc MAD=góc HAD
Xét ΔAHD và ΔAMD có
AH=AM
góc HAD=góc MAD
AD chung
=>ΔAHD=ΔAMD
=>góc AMD=90 độ
Xét ΔAMN vuông tại M và ΔAHC vuông tại H có
AM=AH
góc MAN chung
=>ΔAMN=ΔAHC
=>AN=AC
=>ΔANC cân tại A

a, ΔABD có BA = BD (gt) và ˆABDABD^ = ˆABCABC^ = 60o60o
⇒ ΔABD đều (đpcm)
b, ΔABD đều ⇒ AB = AD
Xét ΔAHB và ΔAHD có:
AH chung; AB = AD (cmt); HB = HD (H là trung điểm của BD)
⇒ ΔAHB = ΔAHD (c.c.c)
⇒ ˆAHBAHB^ = ˆAHDAHD^ mà 2 góc này kề bù
⇒ ˆAHBAHB^ = ˆAHDAHD^ = 90o90o
⇒ AH ⊥ BD (đpcm)
c, ΔABD đều ⇒ AB = BD = AD = 2cm
⇒ HB = HD = 1cm
⇒ HC = BC - HB = 5 - 1 = 4cm
ΔAHB vuông tại H ⇒ AH = √AB2−HB2AB2−HB2 = √22−1222−12 = √33cm
ΔAHC vuông tại H ⇒ AC = √AH2+HC2AH2+HC2 = √3+423+42 = √1919cm
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Xét ΔBAD cân tại B có \(\widehat{ABD}=60^0\)(gt)
nên ΔBAD đều(Dấu hiệu nhận biết tam giác đều)
b) Ta có: ΔBAD đều(cmt)
mà AH là đường trung tuyến ứng với cạnh BD(gt)
nên AH là đường cao ứng với cạnh BD(Định lí tam giác cân)
hay AH\(\perp\)BD(Đpcm)

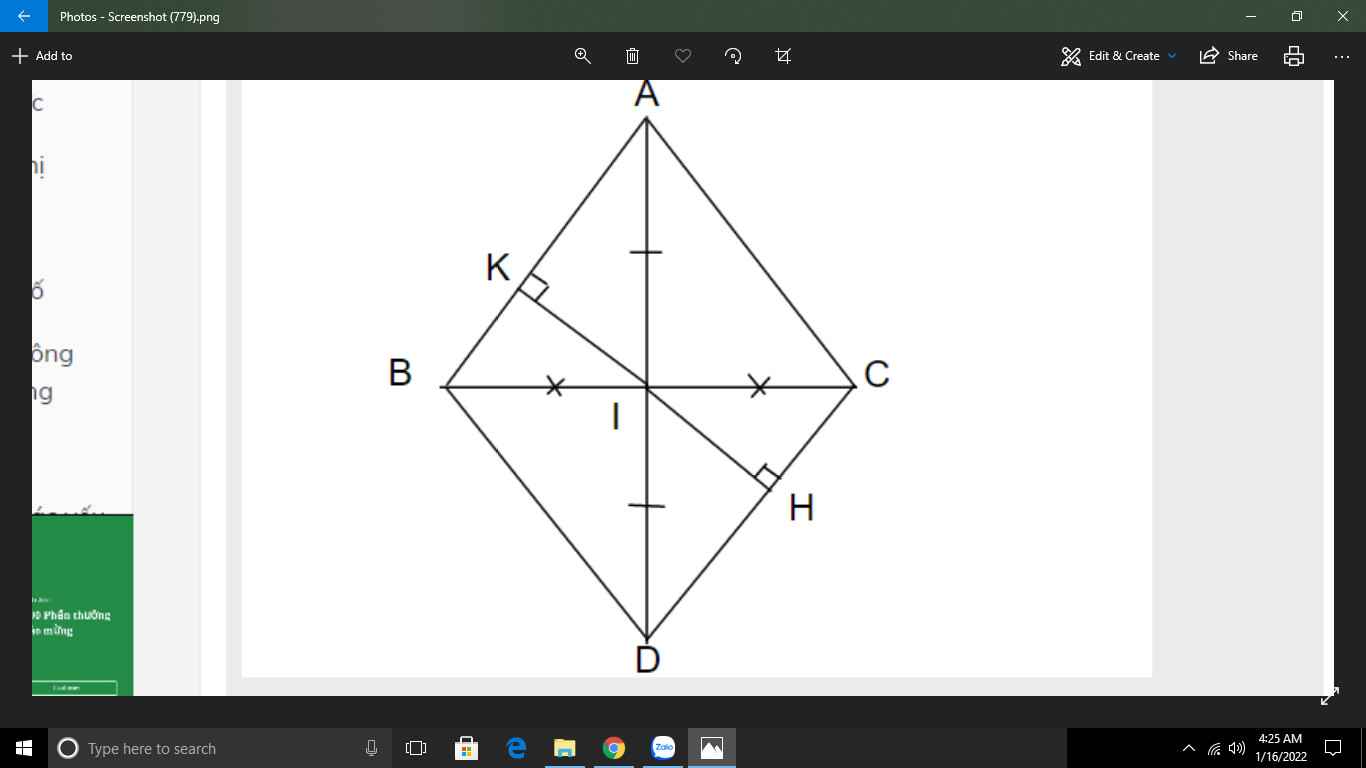
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)