Question

[Nguyễn Minh Hoàng]

Cho tam giác ABC có AB=AC.kẻ BD vuông góc AC tại D,CE vuông góc với AB tại E.BD và CE cắt nhau tại K.Qua B kẻ Bx vuông góc AB,qua C kẻ Cy vuông góc AC.Bx và Cy cắt nhau tại M.Cm A,K,M thẳng hàng

Answer 1

[Nguyễn Lê Phước Thịnh]

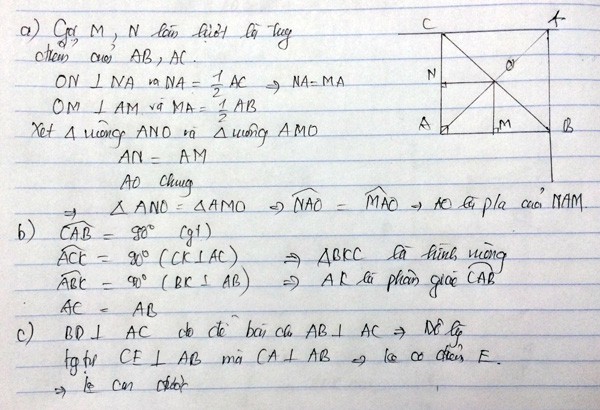
Xét ΔABD vuông tại D và ΔACE vuông tại E có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}\) chung

Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)

⇒AD=AE(hai cạnh tương ứng)

Ta có: AE+EB=AB(E nằm giữa A và B)

AD+DC=AC(D nằm giữa A và C)

mà AB=AC(ΔABC cân tại A)

và AD=AE(cmt)

nên EB=DC

Ta có: ΔABD=ΔACE(cmt)

nên \(\widehat{ABD}=\widehat{ACE}\)(hai góc tương ứng)

hay \(\widehat{EBK}=\widehat{DCK}\)

Xét ΔEBK vuông tại E và ΔDCK vuông tại D có

EB=DC(cmt)

\(\widehat{EBK}=\widehat{DCK}\)(cmt)

Do đó: ΔEBK=ΔDCK(cạnh góc vuông-góc nhọn kề)

⇒BK=CK(hai cạnh tương ứng)

Ta có: \(\widehat{ABC}+\widehat{MBC}=\widehat{ABM}\)(tia BC nằm giữa hai tia BA,BM)

\(\widehat{ACB}+\widehat{MCB}=\widehat{ACM}\)(tia CB nằm giữa hai tia CA,CM)

mà \(\widehat{ABM}=\widehat{ACM}\left(=90^0\right)\)

và \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy trong ΔABC cân tại A)

nên \(\widehat{MBC}=\widehat{MCB}\)

Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)

nên ΔMBC cân tại M(Định lí đảo của tam giác cân)

⇒MB=MC

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: KB=KC(cmt)

nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)

Ta có: MB=MC(cmt)

nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)

Từ (1), (2) và (3) suy ra A,K,M thẳng hàng(đpcm)