Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài cơ bản lớp 7 thì phải :) mình giải chỗ nào không hiểu thì bạn hỏi nha
B C A M \ \ // // K 1 2
Trên tia đối MA lấy điểm K sao cho KM = MA
Xét tam giác MBA và tam giác MCK có:
MB = MC ( Vì M là trung điểm )
\(\widehat{M_1}=\widehat{M_2}\)
MA = MK
\(\Rightarrow\Delta MBA=\Delta MCK\left(c-g-c\right)\)
Mà AB < AC ( gt ) suy ra CK < AC
\(\Rightarrow\widehat{CAK}< \widehat{AKC}\)( góc đối diện với cạnh nhỏ hơn thì góc nhỏ hơn )
\(\Rightarrow\widehat{MAC}< \widehat{BAM}\left(đpcm\right)\)
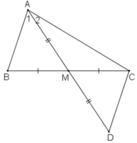
D B A M C
Trên tia đối của MA lấy D sao cho MA = MD
Xét t/g AMB và t/g DMC có:
MA = MD (cách vẽ)
góc AMB = góc DMC (đối đỉnh)
MB = MC (gt)
=> t/g AMB = t/g DMC (c.g.c)
=> AB = CD ; góc BAM = góc CDM
Lại có: AB < AC (gt)
=> CD < AC
=> góc CAM < góc CDA
Mà góc CDA = góc BAM (cmt)
=> góc CAM < góc BAM
Vậy...

Lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của DA
Do đó: ABDC là hình bình hành
=>AB=CD
=>CD<AC
=>\(\widehat{CAD}< \widehat{CDA}\)
mà \(\widehat{CDA}=\widehat{BAM}\)
nên \(\widehat{BAM}>\widehat{CAM}\)


Trên tia đối tia MA lấy điểm D sao cho MD = MA
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (2 cạnh tương ứng)
và ∠D = ∠A1(2 góc tương ứng) (1)
Mà AB < AC (gt)
nên: CD < AC
Trong ΔADC, ta có: CD < AC
Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC) .