S
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
1
25 tháng 5 2021
Gọi (O;R) là đt ngoại tiếp tam giác ABC
Gọi D là gđ của AO và đt (O)
Kẻ đường cao AH => AH vừa là đường cao, đồng thời là đường trung tuyến
ÁP dụng định lí pytago vào tam giác AHB vuông tại H có:\(AH=\sqrt{AB^2-BH^2}=\sqrt{\left(4a\right)^2-\dfrac{BC^2}{4}}\)\(=\sqrt{16a^2-a^2}=a\sqrt{15}\)
Chứng minh được: \(\Delta AHB\sim ACD\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{AD}\) \(\Leftrightarrow AD=\dfrac{AB.AC}{AH}=\dfrac{4a.4a}{a\sqrt{15}}=\dfrac{16a\sqrt{15}}{15}\)
\(\Rightarrow R=\dfrac{AD}{2}=\dfrac{8a\sqrt{15}}{15}\)
S
0
DT
1
Chúc bạn học tốt
CM
4 tháng 3 2018
Chọn đáp án B.
Ta có: A B 2 + A C 2 = B C 2 ( = 100)
Suy ra tam giác ABC vuông tại A.
Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm cạnh huyền BC.
Đường kính đường tròn là : d = BC = 10cm
Suy ra, bán kính đường tròn ngoại tiếp tam giác ABC là R = d/2 = 5cm
TN
24 tháng 5 2016
trong tgiac vuông tâm đường tròn ngoại tiếp chính là trung điểm cạnh huyền
Áp dụng định lý pytago vào tgiac vuông ABC ta có :
\(BC^2\)=\(AC^2\)+\(AB^2\)
\(BC^2\)=\(8^2\)+\(6^2\)
\(BC^2\)=100
BC=10
Vậy bán kính đường tròn ngoại tiếp tgiac ABC là:
10:2=5cm
NT
24 tháng 5 2016
Gọi bk ngoại tiếp là R còn nôi tiếp là r ;p là 1/2 chu vi (= a+b+c/2)
ra có R=BC/2=5
mà S=pr=(6+8+10)/2r=6*8/2=>r=2
CM
4 tháng 5 2019
Chọn đáp án B
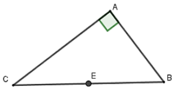
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = BC/2
Theo định lý Pytago ta có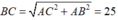 
nên bán kính R = 25/2
