Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

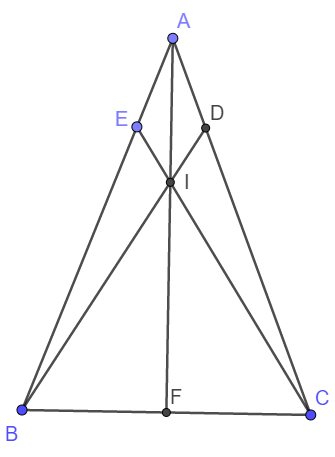
a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

a) Xét tam giác ABM và tam giác ACM, ta có:
AB=AC(gt)
BM=CM(gt)
AM: cạnh chung
Do đó: tam giác ABM = tam giác ACM(c.c.c)
Vậy: Góc AMB = Góc AMC
Mà góc AMB + góc AMC = 180 độ =>
Góc AMB = Góc ACM = 180 độ / 2 = 90 độ
Vậy AM vuông góc với BC
b) Xét tam giác AMD và tam giác AME, ta có:
AD=AE (gt)
Góc DAM = Góc EAM ( theo câu a, cặp góc tương ứng )
AM: cạnh chung
Do đó: Tam giác AMD = tam giác AME (c.g.c)
c) Ta thấy: Góc EDM + Góc KDM = 180 độ ( kề bù )
Vậy ba điểm D,E,K thẳng hàng
=> tam giác ABC cân tại A
Xét ABM và ACM có:
AM chung
AB = AC
A1 = A2 (tam giác ABC cân tại A)
Vậy tam giác ABM = ACM
M1 = M2 ; M1 + M2 = 180 (2 góc kề bù)
=> M1 = M2 = 90
=> AM vuông góc BC

Bài này easy lắm bạn
B A C D E F I Hình ảnh chỉ mang tính chất minh họa
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé

Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B ( d thuộc AC). Kẻ DEvuông gócBC ( E thuộc BC). Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh rằng:
a) BD là đường trung trực của AF
b) AD < BC
c) Ba điểm E, D, F thẳng hàng