Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N
a) Xét \(\Delta ABC\) có :
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A
Mà có : AD là đường trung tuyến trong tam giác cân
=> AD đồng thời là đường trung trực trong tam giác cân (tính chất tam giác cân)
=> \(AD\perp BC\) (đpcm)
b) Xét \(\Delta ANC\) và \(\Delta AMB\) có :
\(\widehat{A}:chung\)
\(AB=AC\left(gt\right)\)
\(\widehat{ANC}=\widehat{AMB}\left(=90^o\right)\)
=> \(\Delta ANC\) = \(\Delta AMB\) (cạnh huyền - góc nhọn)
=> AN = AM (2 cạnh góc vuông)

a: HB=HC=6cm
\(HA=\sqrt{10^2-6^2}=8\left(cm\right)\)
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO đo: ΔABM=ΔACN
Xét ΔBDM vuông tại D và ΔCEN vuông tại E có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔBDM=ΔCEN
c: Xét ΔKBC có
KH là đường cao
KH là đường trung tuyến
Do đó:ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
=>\(\widehat{KCB}=\widehat{DBM}\)
=>\(\widehat{KCB}=\widehat{ECN}\)
=>\(\widehat{KCB}+\widehat{BCE}=180^0\)
=>K,E,C thẳng hàng

a) áp dụng định lý Pytago cho tam giác ABC vuông tại A có:
AB2+AC2=BC2
=> \(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=\sqrt{100-36}=\sqrt{64}=8\left(cm\right)\left(AC>0\right)\)

Xét \(\Delta AMH\)vuông ở H và \(\Delta AMK\)vuông ở K có :
\(\hept{\begin{cases}\widehat{MAH=\widehat{MAK}}\\AM\end{cases}}\)
\(\Rightarrow\)đpcm \(\Rightarrow AH=AK\)
Gọi giao của AM và HK là I
( Rồi xét 2 tam giác AIH và AIK )

Sửa câu a thành CM: BM = CM
A B C D E M K
| GT | △ABC cân tại A ( BAC = 70o) BAM = MAC = BAC/2 MD ⊥ AB (D ME = MK |
KL | a, BM = CM b, △DME cân c, DE // BC d, MDK = ? |
Bài giải:
Vì △ABC cân tại A (gt) => AB = AC và ABC = ACB
Xét △BAM và △CAM
Có: AB = AC (cmt)
BAM = MAC (gt)
AM là cạnh chung
=> △BAM = △CAM (c.g.c)
=> BM = CM (2 cạnh tương ứng)
b, Xét △DBM vuông tại D và △ECM vuông tại E
Có: BM = MC (cmt)
DBM = ECM (cmt)
=> △DBM = △ECM (ch-gn)
=> DM = EM (2 cạnh tương ứng)
Xét △DME có: DM = EM (cmt) => △DME cân tại M
c, Vì △DBM = △ECM (cmt)
=> DB = EC (2 cạnh tương ứng))
Ta có: AD + DB = AB
AE + EC = AC
Mà AB = AC (cmt) ; DB = EC (cmt)
=> AD = AE
Xét △ADE có: AD = AE (cmt) => △ADE cân tại A => ADE = (180o - DAE) : 2 (1)
Vì △ABC cân tại A (gt) => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => ADE = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> DE // BC (dhnb)
d, Ta có: ABC = (180o - BAC) : 2 (cmt)
=> ABC = (180o - 70o) : 2 = 110o : 2 = 55o
Mà ABC = ACB (cmt)
=> ACB = 55o
Xét △BMK và △CME
Có: BM = MC (cmt)
BMK = EMC (2 góc đối đỉnh)
MK = ME (gt)
=> △BMK = △CME (c.g.c)
=> MBK = MCE (2 góc tương ứng)
Mà MCE = 55o
=> MBK = 55o
Ta có: DBK = DBM + MBL = 55o + 55o = 110o
Lại có: DMB = EMC (△DBM = △ECM)
Mà EMC = BMK (2 góc đối đỉnh)
=> DMB = BMK
Ta có: MK = ME (gt)
Mà ME = DM (cmt)
=> DM = MK
Xét △BDM và △BKM
Có: BM là cạnh chung
DMB = BMK (cmt)
MD = MK (cmt)
=> △BDM = △BKM (c.g.c)
=> BD = BK (2 cạnh tương ứng)
=> △BDK cân tại B
=> BDK = (180o - KBD) : 2 = (180o - 110o) : 2 = 70o : 2 = 35o
Ta có: BDM + MDA = 180o (2 góc kề bù)
=> BDK + MDK + 90o = 180o
=> BDK + MDK = 90o
=> 35o + MDK = 90o
=> MDK = 55o
Cho tam giác ABC. Lấy D,E trên cạnh AB sao cho AD=DE=EB. vẽ DG và EF song song với BC (F và G thuộc AC)
a, chứng minh: AG=GF=FC
b, giả sử DG=3cm. Tính BC

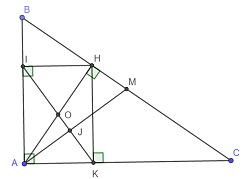
a) Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{IAK}+\widehat{AKH}=270^o\Rightarrow\widehat{IHK}=90^o\)
Vậy nên \(HI\perp HK\)
b) Do IA và HK cùng vuông góc với AC nên IA // HK
Vậy thì \(\widehat{IAH}=\widehat{KHA}\) (So le trong)
Xét tam giác IAH và tam giác KHA có:
\(\widehat{AIH}=\widehat{HKA}=90^o\)
Cạnh AH chung
\(\widehat{IAH}=\widehat{KHA}\)
\(\Rightarrow\Delta AIH=\Delta HKA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow IA=HK.\)
c) Xét tam giác IAH và tam giác HKI có:
\(\widehat{AIH}=\widehat{KHI}=90^o\)
Cạnh IH chung
\(IA=HK\)
\(\Rightarrow\Delta AIH=\Delta KHI\) (Hai cạnh góc vuông)
\(\Rightarrow AH=IK.\)
d) Ta thấy ngay các cặp góc so le trong bằng nhau nên \(\Delta IOA=\Delta KOH\left(g-c-g\right)\Rightarrow OI=OK,OA=OH\)
Xét tam giác vuông IAH có IO là trung tuyến ứng với cạnh huyền nên OH = OA = OI.
Vậy nên OA = OI = OH = OK.
e)
1. Nếu tam giác ABC cân thì AH là đường cao đồng thời trung tuyến. Vậy thì AH = BH = CH.
Xét tam giác cân BHA có HI là đường cao nên đồng thời là đường trung tuyến. Vậy nên I là trung điểm AB.
Hoàn toàn tương tự ta có K là trung điểm AC.
2. Tam giác ABC vuông cân tại A nên \(\widehat{ACB}=45^o\)
IA = AB/2; AK = AC/2 mà AB = AC nên AI = AK.
Vậy thì tam giác IAK cũng vuông cân tại A.
Vậy nên \(\widehat{AKI}=45^o\)
Từ đó ta có \(\widehat{AKI}=\widehat{ACB}=45^o\)
Chúng lại ở vị trí đồng vị nên suy ra IK // BC.
f) Ta có AM = MC nên \(\widehat{MAC}=\widehat{MCA}\)
Lại có \(\widehat{MCA}=\widehat{AHK}\) (Cùng phụ với góc \(\widehat{KHC}\) )
Suy ra \(\widehat{MAC}=\widehat{AHK}\)
Lại có \(\widehat{OKA}=\widehat{OHA}\)
Vậy nên \(\widehat{MAK}+\widehat{OKA}=\widehat{AHK}+\widehat{IHA}=90^o\)
Gọi J là giao điểm của AM và IK thì \(\widehat{AJK}=90^o\) hay \(KI\perp AM\)
 AB) ;ME ⊥ AC (E
AB) ;ME ⊥ AC (E
a) Tam giác vuông ABM và tam giác vuông ACN, có:
AB = AC (gt) và Góc chung Â
=> \(\Delta ABM=\Delta ACN\) (cạnh huyền - góc nhọn) => AM = AN.
Tam giác ABC cân tại A (AB=AC), có:
\(BM\perp AC\) và \(CN\perp AB\), cắt nhau tại H
=> H là trực tâm của tam giác ABC <=> AH là đường cao. (1)
BK = KC (K là trung điểm)
=> AK là trung tuyến => AK là đường cao (tính chất tam giác cân) (2)
Từ (1) và (2) => A, H, K thẳng hàng.