Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC vuông tại A (theo định lý Py-ta-go đảo)
⇒AC⊥AB,⇒AC⊥AB, do đó AC là tiếp tuyến.
Ta có: AB2 + AC2 = 32 + 42 = 25.
BC2 = 52 = 25.
Nên AB2 + AC2 = BC2.
Suy ra tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

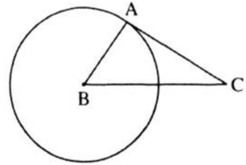
Ta có: AB2 + AC2 = 32 + 42 = 25
BC2 = 52 = 25
Nên AB2 + AC2 = BC2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

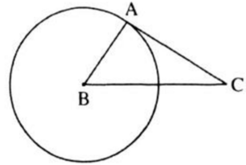
Ta có: A B 2 + A C 2 = 3 2 + 4 2 = 25 B C 2 = 5 2 = 25
Nên A B 2 + A C 2 = B C 2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

a) Xét tam giác ABC có:
\(AB^2+AC^2=8^2+6^2=100=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow AB\perp AC\)
Mà \(A\in\left(C;CA\right)\)
=> AB là tiếp tuyến đường tròn (C)
b) Ta có: AB là tiếp tuyến, C là tâm
=> BC cắt đường tròn

Tam giác ABCABC có:
AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52
Mặt khác: BC^{2}=5^{2}BC2=52
Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.
Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).
CACA vuông góc với bán kính BABA tại AA nên CACA là tiếp tuyến của đường tròn (B)(B).

a. Chứng minh tam giác ABC vuông
+ Xét tam giác ABC có :
AB^2+AC^2=100
BC^2=10^2=100
=> AB^2+ AC^2= 100=BC^2
=> tam giác ABC vuông tại A ( Py-ta-go)
áp dụng định lý py ta go đảo vào tam giác ABC Ta có:
62+82=102⇒AB2+AC2=BC2
⇒tam giác ABC là tam giác vuông tại A
Xét tam giác ABC và tam giác HBA
ta có B là góc chung
góc A = góc H=90 độ
⇒tam giác ABC đồng dạng với tam giác HBA
⇒BCBA =ACHA

Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét (B)có
BA là bán kính
CA\(\perp\)AB tại A
Do đó: CA là tiếp tuyến của (B)
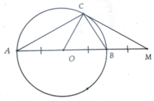
Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
=>AC là tiếp tuyến của (B;BA)
Vì \(BC^2=AB^2+AC^2\) nên tg ABC vuông tại A
Do đó \(BA\perp AC\) hay AC là tt đường tròn (B;BA)