Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì
△
A'B'C' đồng dạng
△
ABC nên 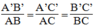
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB + 10,8cm = 16,2 + 10,8 = 27 (cm)
Ta có: 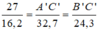
Suy ra: 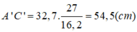
Suy ra: 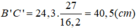

Vì
△
A'B'C' đồng dạng
△
ABC nên 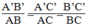
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB - 5,4 = 16,2 - 5,4 =10,8 (cm)
Ta có: 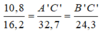
Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)
B'C'= (10,8 . 24,3): 16,2 = 16,2 (cm)

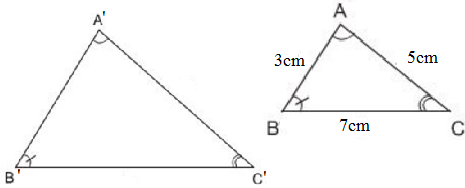
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’ 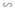 ΔABC ⇒
ΔABC ⇒ 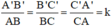
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
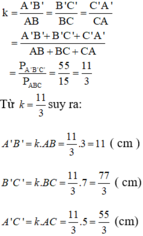

∆ABC ∽ ∆A'B'C' => ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′ = CABCCA′B′C′CABCCA′B′C′
hay 3A′B′3A′B′ = 7B′C′7B′C′ = 5A′C′5A′C′ =

Ta có
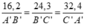
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm

Anh mình nghĩ là như thế này. Mà ko biết đúng hay sai .
Ta có : \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
Suy ra : \(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow B'C'=\frac{5.4,5}{3}=7,5\)
\(C'A'=\frac{7.4,5}{3}=10,5\)
Chu vi tam giác A'B'C' là :
4,5 + 7,5 + 10,5 = 22,5 cm
Đ/s : 22,5 cm

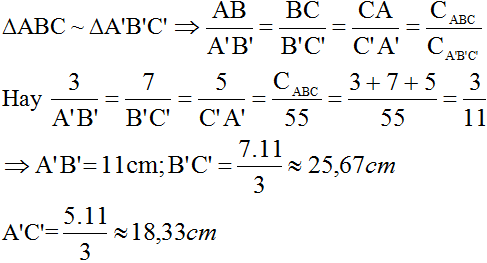

Theo giả thiết ta có: \(A'B'=AB+3=5+3=8\left(cm\right)\).
Do \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
\(\Rightarrow\dfrac{7}{A'C'}=\dfrac{9}{B'C'}=\dfrac{5}{8}\Rightarrow\left\{{}\begin{matrix}A'C'=\dfrac{7.8}{5}=\dfrac{56}{5}\left(cm\right)\\B'C'=\dfrac{9.8}{5}=\dfrac{72}{5}\left(cm\right)\end{matrix}\right.\).