Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(AB = c = 5,{\rm{ }}AC = b = 6,{\rm{ }}BC = a = 7\).
\( \Rightarrow \cos A = \frac{{{6^2} + {5^2} - {7^2}}}{{2.5.6}} = \frac{1}{5}\)
Chú ý
Từ định lí cosin, ta suy cách tìm góc khi biết độ dài 3 cạnh
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\;\cos C = \frac{{{b^2} + {a^2} - {c^2}}}{{2ab}}.\)

Xét ΔABC có
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{8^2+6^2-AB^2}{2\cdot6\cdot8}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(100-AB^2=48\sqrt{3}\)
=>\(AB=\sqrt{100-48\sqrt{3}}\simeq4,11\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinC\)
\(=\dfrac{1}{2}\cdot6\cdot8\cdot sin30=3\cdot8\cdot\dfrac{1}{2}=3\cdot4=12\)
\(AB=\sqrt{AC^2+BC^2-2.AC.BC.cosC}\)
\(AB=4,11\)
\(S_{ABC}=\dfrac{1}{2}. AC.BC.sinC\)
\(S_{ABC}=\dfrac{1}{2}. 8.6.sin 30^o\)
\(S_{ABC}=12\)

Áp dụng định lý hàm cosin:
\(AC=\sqrt{AB^2+BC^2-2AB.BC.cosB}=\sqrt{2^2+3^2-2.2.3.cos60^0}=\sqrt{2}\)
Diện tích tam giác:
\(S=\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}.2.3.sin60^0=\dfrac{3\sqrt{3}}{2}\)

Kẻ đường cao AH
\(\Rightarrow\Delta AHB\text{ vuông cân tại }H\\ \Rightarrow AH=HB=\cos45^0\cdot AB=\dfrac{\sqrt{2}}{2}\cdot4=2\sqrt{2}\\ \Rightarrow HC=BC-HB=5-2\sqrt{2}\\ \Rightarrow AC=\sqrt{HC^2+AH^2}\approx3,57\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot2\sqrt{2}\cdot5=5\sqrt{2}\left(đvdt\right)\)

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)

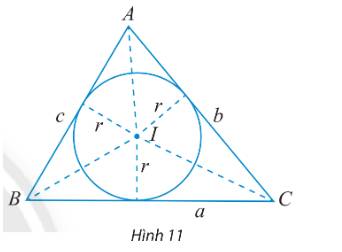
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)

Áp dụng hệ quả định lí cô sin trong tam giác ta có:
cos A = 2 2 + 2 2 − 1 2 2.2.2 = 7 8
Chọn C.
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{2}{3}\)
\(sinA=\sqrt{1-cos^2A}=\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC.sinA=6\sqrt{5}\)