Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/. _Kẻ pg AD và đ/cao AE (D ; E thuộc BC) ta thấy AG/AE=2/3_bt:(1)
Trong tg ABC vớí pg AD ta có : DB/DC= AB/AC=6/12=1/2 <=> BD=3 ; DC=6 (cm)
Trong tg ABD với pg BI ta có : IA/IB=AB/BD =3/6 <=>AI/AD=2/3 -bt:(2). từ (1) & (2)suy ra đpcm
góc AED=^ACB=48 độ ( hai góc đều cọng với góc^BED thì =180 độ

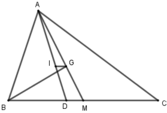
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A

cho tam giác abc có AB=12cm BC=15cm AC=18cm gọi I là giao điểm của các đường phân giác G là trong tâm của tam giác ABC
a) chứng minh IG//BC
b) tính IG
ai giải giùm mình cho
mình có câu tương tự

a) Gọi tam giác ACB có AN là phân giác và trung tuyến AM
\(\frac{NB}{NC}=\frac{AB}{AC}=\frac{6}{12}=\frac{1}{2}\)
\(\Rightarrow NB=\frac{NC}{2}\)
NC+NB=NC+0,5NC=1,5NC=BC=9 (cm) <=> NC=6cm
=>NB=3cm
Ta có: \(\frac{NB}{BC}=\frac{3}{9}=\frac{1}{3}\)
Xét tam giác ABN có BI là phân giác
=> \(\frac{AI}{IN}=\frac{BA}{BN}=\frac{6}{3}=2\)
Lại có AM là trung tuyến nên \(\frac{AG}{GM}=2\)
\(\Rightarrow\frac{AG}{GM}=\frac{AI}{IN}=2\)
=> IG//BC(Talet đảo) (đpcm)
b) \(BM=\frac{9}{2}=4,5\left(cm\right)\)
=> MN=4,5 -3=1,5 (cm)
\(\frac{AG}{AM}=\frac{2}{3}=\frac{IG}{MN}\)(Định lý Talet)
\(\Rightarrow\frac{2}{3}=\frac{IG}{1,5}\Rightarrow IG=1cm\)
