K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

21 tháng 4 2019
A B C D E F G H I O
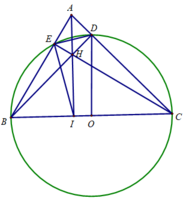
Gọi GE,FD cắt đường tròn (O) lần thứ hai tại H,I.
Ta thấy F nằm trên trung trực BD => \(\Delta\)BDF cân tại F. Mà \(\Delta\)BDF ~ \(\Delta\)IDA (g.g) nên \(\Delta\)IDA cân tại A
Hay AI = AD. Tương tự ta có AH = AE. Do AD = AE nên AH = AD = AE = AI => A cách đều 4 điểm H,D,E,I
=> Tứ giác DEIH nội tiếp. Vậy thì ^DEH = ^DIH = ^HIF = ^HGF => DE // FG (2 góc đồng vị bằng nhau) (đpcm).

CM
24 tháng 1 2019
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256