Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
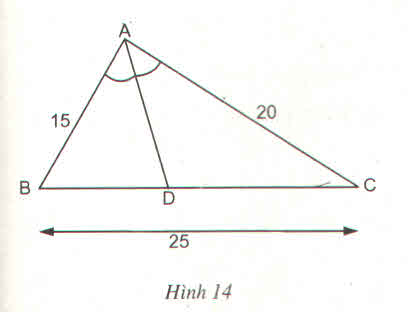
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: \(\frac{DB}{DC}=\frac{AB}{AC}\)(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
uy ra: \(\frac{DB}{DB+DC}=\frac{15}{15+20}\)(tính chất tỉ lệ thức)
Suy ra: \(\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}cm\)
\(\Rightarrow DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}cm\)
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
Suy ra :\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mà\(\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ADC}}=\frac{3}{4}\)
a: Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{12}=\dfrac{CD}{14}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{7}\)
mà AD+CD=AC=9cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{7}=\dfrac{AD+CD}{6+7}=\dfrac{9}{13}\)
=>\(AD=\dfrac{9}{13}\cdot6=\dfrac{54}{13}\left(cm\right);CD=\dfrac{9}{13}\cdot7=\dfrac{63}{13}\left(cm\right)\)
b: Sửa đề: b) Tính tỉ số diện tích của tam giác ABD và tam giác BDC
Vì \(\dfrac{AD}{6}=\dfrac{CD}{7}\)
nên \(\dfrac{AD}{CD}=\dfrac{6}{7}\)
=>\(\dfrac{S_{ABD}}{S_{CBD}}=\dfrac{6}{7}\)
=>\(S_{ABD}=\dfrac{6}{7}\cdot S_{CBD}\)
a) Xét tam giác BAD và CAD có:
AB=AC=14cm
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác)
AD cạnh chung
=> \(\Delta BAD=\Delta CAD\left(c.g.c\right)\)
=> BD=CD
Mà BD+CD=BC=12 cm
=> BD=DC=12:2=6(cm)
b) Vì AB=AC, BD=DC
=> AD là đường trung trực của BC
=> AD _|_ BC
=> \(S_{\Delta ABD}=\frac{1}{2}AD\cdot BD;S_{\Delta CAD}=\frac{1}{2}AD\cdot DC\)
\(\frac{S_{\Delta ABD}}{S_{\Delta CAD}}=\frac{AD\cdot BD}{AD\cdot DC}=\frac{AD}{DC}=1\)
Cho tam giác ABC có AB = 16cm, AC = 24cm, BC = 30cm. Đường phân giác của góc BAC cắt cạnh BC tại D.Qua D kẻ DE //AB (E AC) a/ Tính độ dài các đoạn thẳng DB, DC và DE. b/ Tính tỉ số diện tích của hai tam giác ABD và ACD.
ta co: AB2+AC2=100 Ma BC2=100
\(\Rightarrow\Delta ABC\)vuong tai A
A, Trong \(\Delta ABC\)co AD la phan giac
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tinh chat duong phan giac)
\(\Rightarrow\frac{AB}{AB+AC}=\frac{BD}{BD+DC}\)\(\Rightarrow\frac{8}{8+6}=\frac{BD}{10}\Rightarrow BD=\frac{8.10}{14}=\frac{40}{7}cm\)
ta co: BD+DC=BC\(\Rightarrow DC=BC-BD=10-\frac{40}{7}=\frac{30}{7}cm\)
B, Ke duong cao AH
ta co: \(S_{\Delta ABD}=\frac{1}{2}AH.BD\)va \(S_{\Delta ACD}=\frac{1}{2}AH.DC\)
\(\Rightarrow\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}=\frac{40}{7}:\frac{30}{7}=\frac{4}{3}\)
a,theo tính chất đường phân giác ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{14}{16}=\frac{7}{8}\)
=> BD=7/8 CD
Mà BD+CD=BC=12
<=> 7/8CD+CD=12
<=> CD=6,4cm
=> BD=5.6cm
cau b)
ta có tgiac abc vuông tại a(gthiet)
theo định lí pi ta go ta có:
BC^2=AC^2+AB^2=81+144=225
suy ra BC=15
*BD=?
ta có AD la p/giac (giả thiết)
suy ra BD/DC=AB/AC (tính chất đương phân giác)
suy ra BD/BD+DC=9/9+12=3/7
suy ra BD/BC=3/7
suy ra BD=15.3/7=45/7
DC=BC-BD=15-45/7=60/7
*Câu c)............
a, Vì AD là phân giác nên \(\frac{AB}{AC}=\frac{DB}{DC}\Rightarrow\frac{DC}{AC}=\frac{DB}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{DB}{AB}=\frac{BC}{AB+AC}=\frac{10}{15}=\frac{2}{3}\Rightarrow DC=6cm;DB=4cm\)
Lời giải:
a. $AB=AC=14$ cm nên $ABC$ là tam giác cân tại $A$
Do đó đường phân giác $AD$ đồng thời là đường trung tuyến
$\Rightarrow BD=DC=\frac{BC}{2}=6$ (cm)
b.
$\frac{S_{ABD}}{S_{ACD}}=\frac{BD}{CD}=1$
Hình vẽ: