Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔACB cân tại C
mà CN là đường trung tuyến
nên CN là đường cao
Ta có: ΔACB cân tại B
mà BM là đường trung tuyến
nên BM là đường cao
Xét ΔIAB có
IN là đường cao
IN là đường trung tuyến
Do đó: ΔIAB cân tại I
=>IA=IB(1)
Xét ΔIAC có
IM là đường cao
IM là đường trung tuyến
Do đó: ΔIAC cân tại I
=>IA=IC(2)
Từ (1) và (2) suy ra IA=IB=IC

a)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
b)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
c)Từ (2) và (4) suy ra MB+MC<AB+AC
d)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

CM BNC=CMB
MC=BN ; \(\widehat{B}=\widehat{C}\) ; BC chung
\(\Rightarrow\)BM=CN
CM ABM=ACN
AB=AC ; AM=AN ; \(\widehat{A}\) chung
\(\Rightarrow\)ABM =ACN \(\Rightarrow\) \(\widehat{ABM}=\widehat{ACN}\)
b \(\widehat{ABM}=\widehat{ACN}\) \(\Rightarrow\)\(\widehat{ABI}=\widehat{ACI}\);
\(\Rightarrow\) \(\widehat{AMB}=\widehat{ANC}\)\(\Rightarrow\)\(\widehat{BMC}=\widehat{CNB}\)
Xét BIN vs CIM : BN=CM ; \(\widehat{ACM}=\widehat{ACN};\)\(\widehat{BMC}=\widehat{CNB}\)
\(\Rightarrow\) IB=IC \(\Rightarrow\)IBC cân
c, Xét AIB và AIC : IB =IC ; \(\widehat{ABI}=\widehat{ACI};AB=AC\)
\(\Rightarrow\) \(\widehat{BAI}=\widehat{CAI}\)\(\Rightarrow\)AI pg góc A
d, xét BAD và CAD
góc BAI = CAI ; AB=AC ; AD chung
\(\Rightarrow\)góc ADB = ADC mà chúng cộng nhau = 180 \(\Rightarrow\)\(\widehat{D}\)= 90

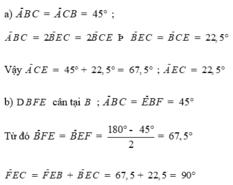
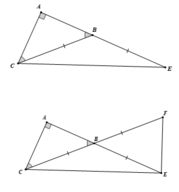
\(\left\{{}\begin{matrix}AC=BC\\AN=NB\\CN\text{ chung}\end{matrix}\right.\Rightarrow\Delta ACN=\Delta BCN\left(c.c.c\right)\\ \Rightarrow\widehat{ANC}=\widehat{BNC}\\ \text{Kết hợp với }AN=NB;NI\text{ chung}\\ \Rightarrow\Delta AIN=\Delta BIN\left(c.g.c\right)\\ \Rightarrow AI=BI\left(1\right)\)
Cmtt \(\Rightarrow\Delta ABM=\Delta CBM\left(c.c.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{CMB}\\ \Rightarrow\Delta AIM=\Delta CIM\\ \Rightarrow AI=CI\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AI=BI=CI\)