Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của CK
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2MC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥BC
mà BC//AK
nên AM⊥AK
hay \(\widehat{MAK}=90^0\)

A C B M N K
a) Xét 2 tam giác ABM và ACM:
+ MB=MC
+ AB=AC
+ Cạnh AM chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b) Xét 2 tam giác ANK và BNC
+ NK=NC
+ NA=NB
+ Góc ANK = góc BNC ( hai góc đối đỉnh )
\(\Rightarrow\Delta ANK=\Delta BNC\left(c.g.c\right)\)
\(\Rightarrow AK=BC\)( hai cạnh tương ứng )
Mà M là trung điểm của BC nên BC=2MC
\(\Rightarrow AK=2.MC\)
c) Ta có \(\widehat{AKN}=\widehat{BCN}\)( hai góc tương ứng của hai tam giác bằng nhau )
Mà hai góc AKN và BCN là cặp góc so le trong
\(\Rightarrow AK//BC\)
Vì hai tam giác ABM=ACM nên góc AMB= góc AMC ( hai góc tương ứng )
Mà góc AMB + AMC = 180 độ ( kề bù )\
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)
\(\Rightarrow AM\perp BC\)
Mà AK//BC
\(\Rightarrow AM\perp AK\)

Bài 2
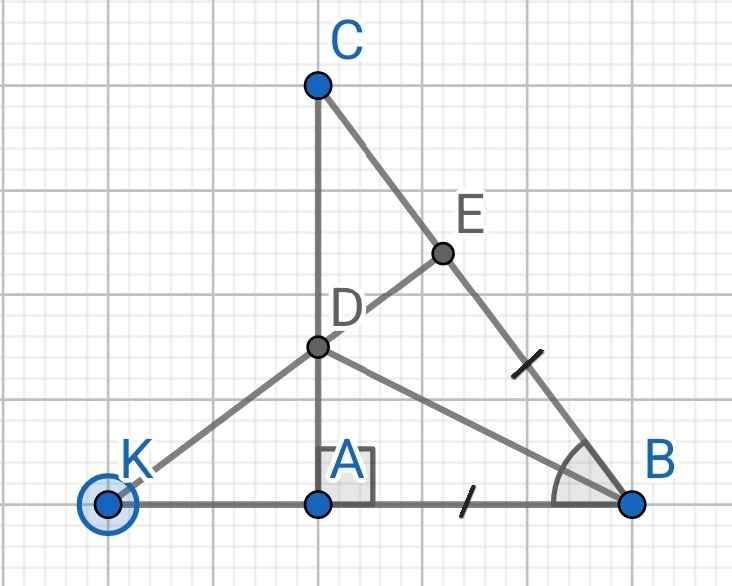
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BE
⇒ DE ⊥ BC
c) Do DE ⊥ BC (cmt)
⇒ ∠DEC = 90⁰
⇒ ∆DEC vuông tại E
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ADK và ∆DEC có:
AD = DE (cmt)
∠ADK = ∠EDC (đối đỉnh)
⇒ ∆ADK = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AK = EC (hai cạnh tương ứng)
Ta có:
AB = BE (gt)
AK = EC (cmt)
⇒ AB + AK = BE + EC
⇒ BK = BC
Bài 1
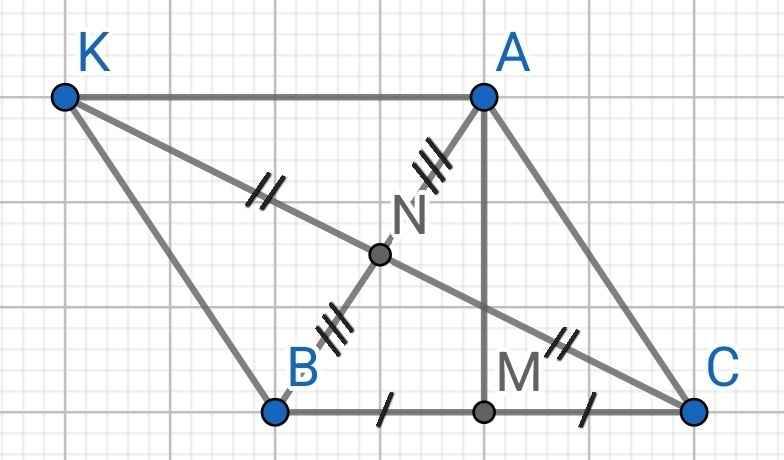 a) Xét ∆ABM và ∆ACM có:
a) Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (gt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do M là trung điểm của BC
⇒ BC = 2MC
Xét ∆ANK và ∆BNC có:
AN = BN (gt)
NK = NC (gt)
∠ANK = ∠BNC (đối đỉnh)
⇒ ∆ANK = ∆BNC (c-g-c)
⇒ AK = BC (hai cạnh tương ứng)
Mà BC = 2MC (cmt)
⇒ AK = 2MC
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∆AMB vuông tại M
⇒ ∠ABM + ∠BAM = 90⁰ (1)
Do ∆ANK = ∆BNC (cmt)
⇒ ∠KAN = ∠NBC (hai góc tương ứng)
⇒ ∠KAN = ∠ABM (2)
Từ (1) và (2) ⇒ ∠MAK = ∠KAN + ∠BAM = 90⁰

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của CK
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2MC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥BC
mà BC//AK
nên AM⊥AK
hay \widehat{MAK}=90^0MAK=900
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của KC
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2xMC