Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

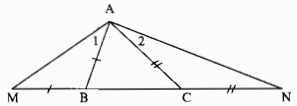
Trong ∆ABC có AB < AC
⇒ góc ABC= góc ACB (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
⇒ góc ∆ABM cân tại B
⇒ góc M = góc A1(tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
góc ABC= góc M+ góc A1
Suy ra: góc M=12 góc ABC (2)
Ta có: AC = CN (gt)
⇒ ∆CAN cân tại C⇒ góc N= góc A2 (tính chất tam giác cân)
Trong ∆CAN ta có góc ACB là góc ngoài tại đỉnh C.
⇒góc ACB= góc N+ góc A2
Suy ra: góc N=12 góc ACB (3)
Từ (1), (2) và (3) suy ra: góc M > góc N
b) Trong ∆AMN ta có: góc M> góc N

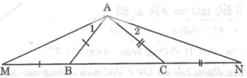
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)
Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

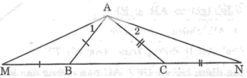
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .

a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC