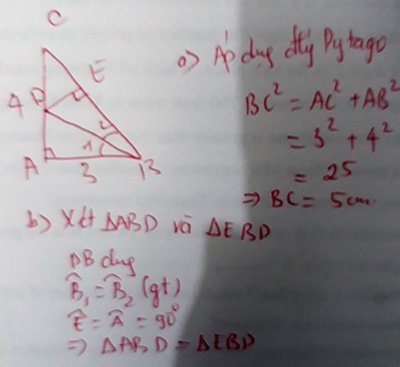Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BC
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay MB=MC
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác và cũng là đường cao
b: Ta có: AB=CD
mà AB=AC
nên CD=AC
=>ΔACD cân tại C
mà CM là đường cao
nên M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
a) Xét \(\Delta AMBva\Delta AMC\) có
\(\hept{\begin{cases}AB=AC\left(gt\right)\\chungAM\\\widehat{BAM}=\widehat{MAC}\left(gt\right)\end{cases}\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\left(ĐPCM\right)}\)
b) từ 2 tam giác trên = nhau =>BM=CM
xét tam giác BAM và tam giác CEM có
\(\hept{\begin{cases}BM=CM\left(cmt\right)\\AM=ME\left(gt\right)\\\widehat{BMA}=\widehat{EMC}\left(đoi-đinh\right)\end{cases}}\Rightarrow\Delta AMB=\Delta EMC\left(c-g-c\right)\Rightarrow\widehat{BAM}=\widehat{MEC}\left(ĐPCM\right)\)
c) từ hai góc trên = nhau, mà 2 góc đó ở vị trí so le trong =>AB//CE => AK vuông góc với CE => tam giác ACK vuông tại K
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔABM=ΔACM
Ta có hình vẽ trên :
a) Xét 2 tam giác ABM và tam giác ACM có:
AB = AC (gt)
AM là cạnh chung
BM = MC (gt)
=>. tam giác ABM = tam giác ACM (c-c-c)
=> góc A1 = góc A2 (2 góc tương ứng)
=> AM là tia phân giác của góc BAC
b) Vì tam giác ABM = tam giác ACM
nên góc AMB = góc AMC (2 góc tương ứng)
mà góc AMB + góc AMC = 180 độ
=> góc AMB = góc AMC = 180/ 2 = 90 độ
=> AM vuông góc vói BC
c) Xét 2 tam giác vuông AMB và tam giác và tam giác DMC có:
MA =DM (gt)
BM = MC (gt)
=> tam giác AMB = tam giác DMC (2 cạnh góc vuông)
=> AB = DC (2 cạnh tương ứng)
CAU A: XÉT TAM GIÁC ABM VÀ NMC CÓ:
BM=MC; GÓC BMA= NMC;AM=MN TỪ TRÊN SUY RA TAM GIÁC ABM= NMC
CÂU B
a: Xét tứ giác ABNC có
M là trung điểm của BC
M là trung điểm của AN
Do đó: ABNC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABNC là hình chữ nhật
Suy ra: AB=NC và ΔCAN vuông tại C
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC
a) Xét tam giác MAB và tam giác MCN có
MB =MC ( M là tđ BC)
AM =AN (gt)
AMB = CMD ( 2 góc đối đỉnh )
=> 2 tam giác = nhau (c-g-c)
=> AB =NC (2 cạnh tương ứng)
=> góc BAN = góc ANC (2 góc tương ứng)
mà 2 góc ở vị trí so le trong => AB // NC
=> A + C = 180 ( 2 góc trong cùng phía bù nhau)
=> 90 + c = 180 => góc C=90
xét tam giác ACN có góc C =90 => tma giác ACN vuông tại C
b) Xét tam giác ABC vuông tại A có M là trung điểm BC => AM là trung tuyến => AM = BM = CM =1/2 BC(tc)
c) ta xét tam giác BAN có : AM =MN => M là trung điểm của AN => BM là trung tuyến của AN
mà BM = AM (cmt ) => BM=AM=MN=1/2AN
=> tam giác ABN vuông tại B => AB vuông góc với BN
mà MK vuông góc với BN (gt)=> AB // MK ( từ vuông góc -> //)
mà AB vuông góc AC => MK vuông góc với AC (từ vuông góc -> //)
ta lại có MI cũng vuông góc với AC (gt)
=> M,K,I thẳng hàng (tiên đề ơ clits)