Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E
Vì AD là phân giác \(\widehat{BAC}\left(gt\right)\)
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tính chất đường phân giác tam giác )
\(\Rightarrow\frac{AB}{AC+AB}=\frac{BD}{BD+DC}\)
\(\Rightarrow\frac{12}{12+20}=\frac{BD}{BC}\)
\(\Rightarrow\frac{12}{32}=\frac{BD}{28}\)
\(\Rightarrow BD=\frac{12.28}{32}=10,5cm\)
Ta có : \(BD+DC=BC\left(D\in BC\right)\)
\(\Rightarrow DC=28-10,5=17,5cm\)
Xét \(\Delta ABC\)có \(DE//AB\left(gt\right)\)
\(\Rightarrow\frac{DE}{AB}=\frac{DC}{BC}\)(hệ quả định lí Ta - lét )
\(\Rightarrow DE=\frac{AB.DC}{BC}=\frac{12.17,5}{28}=7,5cm\)
Chúc bạn học tốt !
Tia p/g góc A cắt BC tại D
\(\Rightarrow\)Áp dụng tích chất đường phân giác trong tam giác ta có: \(\frac{BD}{AB}=\frac{DC}{AC}\Leftrightarrow\frac{BD}{12}=\frac{DC}{20}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có: \(\frac{BD}{12}=\frac{DC}{20}=\frac{BD+DC}{12+20}=\frac{28}{32}=\frac{7}{8}\)
\(\Rightarrow\hept{\begin{cases}BD=\frac{7}{8}\times12=10.5cm\\DC=\frac{7}{8}\times20=17.5cm\end{cases}}\)
Vì DE//AB (theo đề bài) \(\Rightarrow\)Nó tạo thành hai tam giác đồng dạng là \(\Delta CDE\)và \(\Delta CBA\)
Nên ta có tỉ lệ các cạnh là: \(\frac{CE}{CA}=\frac{CD}{CB}=\frac{ED}{AB}\Leftrightarrow\frac{DE}{12}=\frac{17.5}{28}=\frac{5}{8}\)
\(\Rightarrow DE=\frac{5}{8}\times12=7.5cm\)
Vậy cạnh DE có độ dài bằng 7.5cm

a: BC=căn 12^2+16^2=20cm
Xét ΔABC có AD là phân giác
nên BD/DC=AB/AC=3/4
=>BD/3=DC/4=(BD+DC)/(3+4)=20/7
=>BD=60/7cm; DC=80/7cm
Xét ΔCAB có ED//AB
nên ED/AB=CD/CB=4/7
=>ED/12=4/7
=>ED=48/7cm
b: S ABC=1/2*12*16=96cm2
BD/BC=3/7
=>S ABD/S ABC=3/7
=>S ABD=288/7cm2

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 21 2 + 28 2 = 1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠ (BAC) nên:
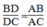 (t/chất đường phân giác)
(t/chất đường phân giác)
Suy ra: 
Hay 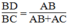
Suy ra: 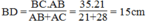
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: 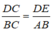 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: 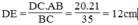

Xét ΔBAC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{12}=\dfrac{CD}{20}\)
mà BD+CD=28cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{20}=\dfrac{BD+CD}{12+20}=\dfrac{28}{32}=\dfrac{7}{8}\)
Do đó: BD=10,5cm; CD=17,5cm
Xét ΔBAC có
DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{BC}\)
\(\Leftrightarrow DE=\dfrac{17.5}{28}\cdot12=7.5\left(cm\right)\)

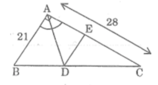
A B C 34 51 D E-
Vì DE // AB, áp dụng hệ quả Ta lét ta có :
\(\frac{ED}{AB}=\frac{CE}{CA}=\frac{CD}{BC}\)(1)
Vì AD là đường phân giác của ^ABC ta có :
\(\frac{AC}{AB}=\frac{CD}{BC}\)(2)
Từ (1) ; (2) Suy ra : \(\frac{ED}{AB}=\frac{AC}{AB}=\frac{CD}{BC}\)
\(\Leftrightarrow\frac{ED}{AB}=\frac{AC}{AB}\Leftrightarrow ED=51\)cm