Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
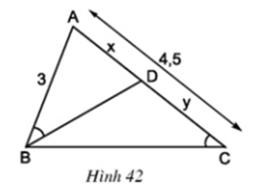
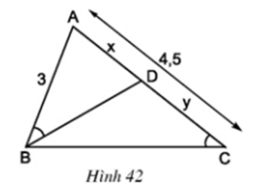
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
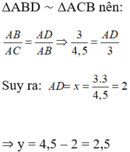
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
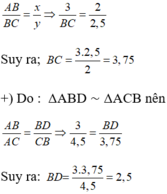
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
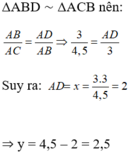
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
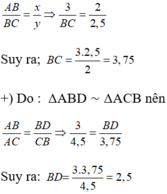
A là phân giác góc BAC => \(\frac{DC}{DB}\)=\(\frac{AC}{AB}\)=\(\frac{16}{12}\)=\(\frac{4}{3}\)=> \(\frac{DC+DB}{DB}\)=\(\frac{4+3}{3}\)=\(\frac{7}{3}\)
=> \(\frac{BC}{DB}\)=\(\frac{7}{3}\)=> DB= \(\frac{3}{7}BC\)=\(\frac{60}{7}\)cm
=> DC = \(\frac{80}{7}\)cm.
Kẻ DE vuông góc với AC
DE vuông góc với AC và AB vuông góc với AC => DE song song với AB
áp dụng hệ quả của định lý Ta-let,ta có;
\(\frac{DE}{AB}\)=\(\frac{CD}{CB}\)=\(\frac{\frac{80}{7}}{20}\)=\(\frac{4}{7}\)=> DE= \(\frac{4}{7}AB\)=\(\frac{48}{7}\)cm
Diện tích tam giác ACD: S\(_{ACD}\)= \(\frac{1}{2}DE.AC\)=\(\frac{1}{2}.\frac{48}{7}.16\)=\(\frac{384}{7}\)cm\(^2\)
Diện tích tam giác ABD: S\(_{ABD}\)= S\(_{ABC}\)-S\(_{ACD}\)= \(\frac{1}{2}AC.AB\)-\(\frac{384}{7}\)= \(\frac{288}{7}\)cm\(^2\)
Tỷ lệ diện tích tam giác ABD và diện tích tam giác ACD là :\(\frac{3}{4}\)
Độ dài cạnh BC là : BC =\(\sqrt{AB^2+AC^2}\)= 20cm
BD=\(\frac{60}{7}cm\)CD =\(\frac{80}{7}cm\)
Chiều cao AH : S\(_{ABC}\)= \(\frac{1}{2}AC.AB\)=\(\frac{1}{2}AH.BC\)=> AH = \(\frac{AB.AC}{BC}\)=\(\frac{12.16}{20}\)=\(\frac{48}{5}\)cm
1)
A B H D c m n
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)
a) Xét 2 tam giác ADB và BCD có:
góc DAB = góc DBC (gt)
góc ABD = góc BDC ( so le trong )
nên tam giác ADB đồng dạng với tam giác BDC.(1)
b) Từ (1) ta được AB/BC = DB/CD = AB/BD
hay ta có; AD/BC = AB/BD <==> 3,5/BC = 2,5/5
==> BC= 3,5*5/2,5 = 7 (cm)
ta cũng có: DB/CD = AB/BD <==> 5/CD = 2,5/5
==> CD = 5*5/2,5 =10 (cm)
c) Từ (1) ta được;
AD/BC = DB/CD = AB/BD hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .
ta nói tam giác ADB đồng giạc với tam giác BCD theo tỉ số đồng dạng là 1/2
mà tỉ số diện tích bằng bình phương tỉ số động dạng
do đó S ADB/ S BCD = (1/2)^2 = 1/4
a)
Vậy ∠EBD = 900
Vậy trong hình vẽ có ba tam giác vuông đó là:
∆ABE, ∆CBD, ∆EBD.
b) ∆ABE và ∆CDB có:
∠A = ∠C = 900
∠ABE = ∠CDB
=> ∆ABE ∽ ∆CDB => AB/CD = AE/CB
=> CD = AB.CB/AE
= 18 (cm)
∆ABE vuông tại A => BE =
= 18 cm
∆EBD vuông tại B => ED =
= 28,2 cm
c) Ta có: 
= 1/2 . 10.15 + 1/2 . 12.18
= 75 + 108 = 183 cm2
SACDE = 1/2 (AE + CD).AC =1/2 (10+18).27=378 cm2
=> SEBD = SEBD – ( SABE + SDBC) = 378 – 183 = 195cm2
