Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ADC và tam giác BAC có
góc C=góc C,AC/BC=DC/AC=2/3
=> tam giác ADC đồng dạng tam giác BAC (c-g-c)
=> AD/AB=AC/BC=> AD=AB.AC/BC=12.18/27=8cm

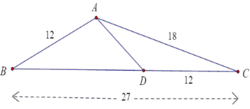
Ta có
A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A
Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)
Nên ΔACB ~ ΔDCA (c.g.c)
⇒ A C D C = A B D A ⇔ 3 2 = 12 D A ⇒ D A = 2.12 3 = 8 c m
Đáp án: D

Tự vẽ hình nhá!
Ta có:
\(\dfrac{AC}{BC}=\dfrac{18}{27}=\dfrac{2}{3}\)
\(\dfrac{CD}{AC}=\dfrac{12}{18}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CD}{AC}\)
Xét \(\Delta ADC\) và \(\Delta BAC\) có:
Góc C chung
\(\dfrac{AC}{BC}=\dfrac{CD}{AC}\)( cmt)
Do đó: \(\Delta ADC\sim\Delta BAC\) (c.g.c)
=> \(\dfrac{AD}{AB}=\dfrac{AC}{BC}\Rightarrow AD=\dfrac{AB.AC}{BC}=\dfrac{12.18}{27}=8\)
Vậy AD = 8(cm)

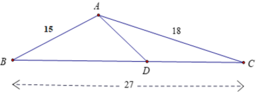
Ta có C D C B = 4 9 ⇒ C D = 4.27 9 = 12
A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A
Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)
Nên ΔACB ~ ΔDCA (c.g.c)
⇒ A C D C = A B D A ⇔ 3 2 = 15 D A ⇒ D A = 2.15 3 = 10 c m
Đáp án: C

a: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
b: Xet ΔABC có HK//BC
nên AH/AB=HK/BC
=>HK/18=6/9=2/3
=>HK=12(cm)
c: Xét ΔABM có HI//BM
nên HI/BM=AI/AM
Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
=>HI/BM=IK/MC
mà BM=CM
nên HI=IK
=>I là trung điểm của HK

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)
\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm
b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)
\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm

a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: CD=căn AC^2+AD^2=13cm