Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.

Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.

Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)

Áp dụng định lí cosin trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\end{array}\)
(trong đó: AB = c, BC = a và AC = b)
Ta được: \(B{C^2} = {a^2} = {8^2} + {5^2} - 2.8.5.\cos {45^o} = 89 - 40\sqrt 2 \)\( \Rightarrow BC \approx 5,7\)
Từ (2) suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\);
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
\( \Rightarrow \cos B \approx \frac{{ - 217}}{{1900}} \Rightarrow \widehat B \approx {97^o} \Rightarrow \widehat C \approx {38^o}\)
Vậy tam giác ABC có BC = 5,7, \(\widehat B = {97^o},\widehat C = {38^o}\)

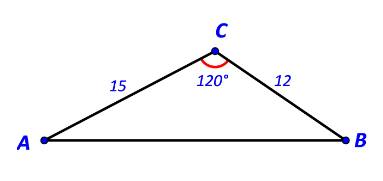
a) Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
b) Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
\( \Rightarrow \widehat A \approx {26^o}\) hoặc \(\widehat A \approx {154^o}\) (Loại)
Khi đó: \(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
c)
Diện tích tam giác ABC là: \(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3 \)

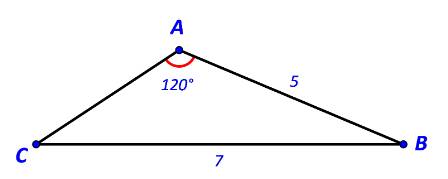
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.

Ta có: \(\widehat B = {65^o},\widehat C = {85^o}.\)
\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}.\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\)
Mà \(\widehat A = {30^o},R = 6.\)
\( \Rightarrow BC = 2.6.\sin {30^o} = 6.\)
Vậy BC = 6.

Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)
Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)
Do đó diện tích tích S của tam giác ABC là:
\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)
Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)