Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

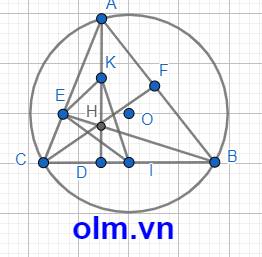
a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)

1: góc ADC=góc AEC=90 độ
=>ADEC nội tiếp
2: góc ABH=90 độ-góc BAC=góc DEA

Hình nếu chị không vẽ được thì hỏi em nhé chị !
Gọi I là trung điểm của BC => I cố định ( vì B,C cố định )
Ta có : AG = 2.OI ( theo bổ đề 7 )
Lại có AM = AH nên AM = 2.OI ( 1 )
Trên tia IO lấy điểm K sao cho OK = 2. OI ( 2 )
=> K cố định ( vì O,I cố định )
Từ ( 1 ) ( 2 ) => AM = KO mà AM// KO
( vì cùng vuông góc với BC ) .
Do đó AMKO là hình bình hành nên KM = OA = R : không đổi
Vậy khi A thay đổi trên cung lớn BC thì điểm M đi động trên đường tròn cố định ( K ; R ) => đpcm

A B C O I G J S K H L A' M N
a) Đặt J là trung điểm cạnh BC. Theo quan hệ vuông góc giữa đường kính và dây ta có ^OIC = ^OJC = 900
Vậy I thuộc đường tròn đường kính OC cố định (đpcm).
b) Kẻ đường kính BK của (O). d cắt CK tại điểm S. Ta có AK vuông góc AB, IS vuông góc AB
Suy ra IS // AK. Vì I là trung điểm cạnh AC của tam giác AKC nên S là trung điểm CK cố định (đpcm).
c) OJ cắt (O) tại hai điểm phân biệt là A' và L (A' thuộc cung lớn BC). Hạ AH vuông góc BC
Ta thấy \(AH+JL\le AL\le2R=A'L\Rightarrow AH\le A'L-JL=A'J\)
Suy ra \(S=\frac{AH.BC}{2}\le\frac{A'J.BC}{2}\)(không đổi). Vậy S lớn nhất khi A trùng A'.
d) Trên đoạn JB,JC lấy M,N sao cho JM = JN = 1/6.BC. Khi đó M,N cố định.
Đồng thời \(\frac{JG}{JA}=\frac{JM}{JB}=\frac{JN}{JC}=\frac{1}{3}\). Suy ra ^MGN = ^BAC = 1/2.Sđ(BC (Vì GM // AB; GN // AC)
Vậy G là các điểm nhìn đoạn MN dưới một góc không đổi bằng 1/2.Sđ(BC, tức là một đường tròn cố định (đpcm).