Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có: BC2 = 62 = 36
AC2 + AB2 = (4√2)2 + 22 = 36
=> tam giác ABC vuông tại A (Py Ta Go đảo)
Sử dụng TSLG để tính góc B
Tính AM = BC - BM = 6 - 2 = 3 cm

\(BM=\dfrac{1}{2}BC=3\)
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cos60^0}=\sqrt{19}\)
\(BN=\dfrac{\sqrt{2\left(AB^2+BM^2\right)-AM^2}}{2}=\dfrac{7}{2}\)

Câu 1:
Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\)
Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\)
Câu 2: Ta có:
\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)
\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)
\(\Rightarrow m_a\approx6,3\)
Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\)
\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\)

Chọn A.
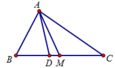
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
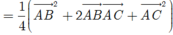
Theo câu trên ta có ![]() nên
nên
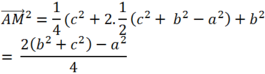
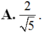
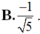
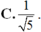
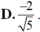
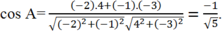
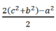
áp dụng hệ quả của cosin
cosA=\(\dfrac{AC^2+AB^2-BC^2}{2.AC.AB}=\dfrac{\left(4\sqrt{2}\right)^2+2^2-6^2}{2.4\sqrt{2}.2}\)=0=>A=90
nửa chu vi
p=\(\dfrac{6+4\sqrt{2}+2}{2}=4+2\sqrt{2}\)
Diện tích của tam giác
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(S=\sqrt{4+2\sqrt{2}\left(4+2\sqrt{2}-6\right)\left(4+2\sqrt{2}-4\sqrt{2}\right)\left(4+2\sqrt{2}-2\right)}\)
=4.2
\(S=pr\)
\(=>r=\dfrac{S}{p}\)=0.6
\(S=\dfrac{1}{2}ca.sinB\)
\(=>4.2=\dfrac{1}{2}.12.sinB\)
=> B=44