Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
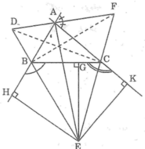
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
a/ Xét tg BIC có
\(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\dfrac{\widehat{B}}{2}-\dfrac{\widehat{C}}{2}=\)
\(=180^o-\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=180^o-\left[\dfrac{180^o-\widehat{A}}{2}\right]=90^o+\dfrac{\widehat{A}}{2}\left(dpcm\right)\)
b/ Để c/m câu này ta chứng minh bài toán phụ: " Hai đường phân giác ngoài của 2 góc với đường phân giác trong của góc còn lại đồng quy"
Có hai đường phân giác của các góc ngoài của góc B và góc C cắt nhau tại J.
Từ J dựng các đường vuông góc với AB; AC; BC cắt 3 cạnh trên lần lượt tại D; E; F
Vì J thuộc đường phân giác của \(\widehat{DBC}\) nên JD=JF
Vì J thuộc đường phân giác của \(\widehat{ECB}\) nên JE=JF
(Mọi điểm thuộc đường phân giác của một góc thì cách đều hai cạnh của góc)
=> JD=JE
Xét tg vuông ADJ và tg vuông AEJ có
ẠJ chung; JD=JE (cmt) => tg ADJ = tg AEJ (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{DAJ}=\widehat{EAJ}\) => Ạ là phân giác của góc \(\widehat{BAC}\)
Áp dụng vào bài toán:
Nối AJ => AJ là phân giác của \(\widehat{BAC}\) => AJ phải đi qua I (Trong tg 3 đường phân giác trong đồng quy) => A; I; J thẳng hàng
c/ Vì J; H; K bình đẳng nên B; I; K thẳng hàng và C; I; H thẳng hàng
=> AJ; BK; CH đồng quy tại I
Xét ΔABC có \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ABC}+\widehat{ACB}=180^0-30^0=150^0\)
=>\(2\cdot\left(\widehat{KBC}+\widehat{KCB}\right)=150^0\)
=>\(\widehat{KBC}+\widehat{KCB}=75^0\)
XétΔKBC có \(\widehat{KBC}+\widehat{KCB}+\widehat{BKC}=180^0\)
=>\(\widehat{BKC}=180^0-75^0=105^0\)
Vì BK và BH là hai tia phân giác của hai góc kề bù
nên BK\(\perp\)BH
=>\(\widehat{KBH}=90^0\)
Vì CK và CH là hai tia phân giác của hai góc kề bù
nên CK\(\perp\)CH
=>\(\widehat{KCH}=90^0\)
Xét tứ giác KBHC có \(\widehat{KBH}+\widehat{KCH}+\widehat{BKC}+\widehat{BHC}=360^0\)
=>\(\widehat{BHC}+105^0+90^0+90^0=360^0\)
=>\(\widehat{BHC}=75^0\)