Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

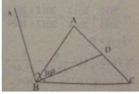
Đây là hình vẽ , lưu ý ở bên dưới ví dụ như ABC là góc ABC
C D A B x x
Vì điểm D thuộc AC nên điểm D nằm giữa 2 điểm A và C
=> AD + CD = AC
Thay số: 4 + 3 = AC
=> 7 = AC
=> AC = 7(cm)
Vậy AC = 7 cm
b) Trên cùng một nửa mặt phẳng bờ chứa tia BA có ABD = 30o, ABC = 55o
=> ABD < ABC
=> ABD + DBC = ABC
Thay số: 30o + DBC = 55o
=> DBC = 55o - 30o
=> DBC = 25o
Vậy DBC = 25o
c) TH1: Tia Bx và BD nằm trên cùng một nửa mặt phẳng bờ chứa tia BA
=> Tia BD nằm giữa hai tia BA và Bx
=> ABD + DBx = ABx
Thay số: 30o + 90o = ABx
=> 120 o = Abx
=> ABx = 120o
TH2: Tia Bx và tia BD nằm trên hai nửa mặt phẳng đối nhau bờ chứa tia BA
=> Tia BA nằm giữa hai tia BD và Bx
=> DBA + ABx = DBx
Thay số: 30o + ABx = 90o
=> ABx = 90o - 30o
=> ABx = 60o
Vậy TH1: ABx = 120o
TH2 : ABx = 60o
Chúc bạn học tốt nha!
bạn ơi đề thiếu phần d
d)trên ab lấy e.cmr 2 đoạn và ce cắt nhau

Tia BD nằm giữa hai tia BA và BC nên
∠ABC = ∠ADB + ∠DBC ; ∠DBC =∠ABC - ∠ADB
∠DBC = 55 0 - 30 0 = 25 0
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có∠ABx = ∠DBx - ∠DBA= 90 0 - 30 0 = 60 0
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có ∠ABx = ∠DBx + ∠DBA= 90 0 + 30 0 = 120 0

a/. AC = AD + DC = 4 + 3 = 7
b/. Vì tia BD nằm giữa 2 tia BA và BC => ABD + DBC = ABC (góc)
=> 30 + DBC = 55
=> DBC = 25
c/. Vì tia BA nằm giữa 2 tia Bx và BD
=> DBA + ABx = xBD
30 + ABx = 90
=> ABx = 90 - 30 = 60
d/. Vì E thuộc AB và D thuộc AC ,mà AB và AC cắt nhau tại A nên CE và BD cắt nhau là hiển nhiên
cho mình hỏi ,làm sao bạn có thể tìm đc tia BA nằm giữa 2 tia Bx và BD

a, Ta có: AD+DC=AC
4+3=AC
AC=7
b, vì BD nằm giữa BA và BC
nên ABD+DBC=ABC(góc)
300+DBC=500
DBC=500-300=200
Tia BD nằm giữa hai tia BA và BC nên
A B C ^ = A D B ^ + D B C ^ ; D B C ^ = A B C ^ - A D B ^
D B C ^ = 55 ° - 30 ° = 25 °
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ - D B A ^ = 90 ° - 30 ° = 60 °
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có A B x ^ = D B x ^ + D B A ^ = 90 ° + 30 ° = 120 °