Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi IK là đường phân giác của \(BIC\)^
Ta có:B^+C^=180-A^=120
\(\Rightarrow DBC\)^+ECB^=120:2=60
\(\Rightarrow\)BIC^=180-60=120
\(\Rightarrow\)BIE^=180-BIC^=180-120=60(kề bù)
Mà BIC^=120\(\Rightarrow\)BIK^=60
Xét t/g BIK và t/g BIE có:
BIE^=BIK^,IBK^=IBE^,BI chung
\(\Rightarrow\)t/g BIK=t/g BIE(g.c.g)
\(\Rightarrow IE=IK\)
Chứng minh tương tự \(\Rightarrow ID=IK\)
\(\Rightarrow ID=IE\)
Tự vẽ hình

Kẻ IG là phân giác của góc BIC
góc IBC+góc ICB=1/2(góc ABC+góc ACB)=1/2x120=60 độ
=>góc BIC=120 độ
=>góc EIB=góc BIG=góc CIG=góc DIC=60 độ
Xét ΔIEB và ΔIGB có
góc EIB=góc GIB
IB chung
góc IBE=góc IBG
Do đó: ΔIEB=ΔIGB
Suy ra: IE=IG(1)
Xét ΔIGC và ΔIDC có
góc GIC=góc DIC
IC chung
góc GIC=góc DIC
Do đó: ΔIGC=ΔIDC
Suy ra: IG=ID
=>ID=IE
Kẻ IG là phân giác của góc BIC
góc IBC+góc ICB=1/2(góc ABC+góc ACB)=1/2x120=60 độ
=>góc BIC=120 độ
=>góc EIB=góc BIG=góc CIG=góc DIC=60 độ
Xét ΔIEB và ΔIGB có
góc EIB=góc GIB
IB chung
góc IBE=góc IBG
Do đó: ΔIEB=ΔIGB
Suy ra: IE=IG(1)
Xét ΔIGC và ΔIDC có
góc GIC=góc DIC
IC chung
góc GIC=góc DIC
Do đó: ΔIGC=ΔIDC
Suy ra: IG=ID
=>ID=IE
=)))))))))))))))))))))

A B C D E I F
Do \(\widehat{BAC}=60^o\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-60^o=120^o\).
Suy ra \(\widehat{IBC}+\widehat{ICB}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=60^o\).
Suy ra \(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=120^o\).
Vì vậy \(\widehat{EIB}=\widehat{DIC}=180^o-120^o=60^o\).
Kẻ tia phân giác IF của góc BIC (F thuộc BC). Suy ra \(\widehat{BIF}=\widehat{FIC}=120^o:2=60^o\).
Xét tam giác EIB và tam giác FIB có:
BI chung.
\(\widehat{EBI}=\widehat{IBF}\)
\(\widehat{EIB}=\widehat{FIB}\)
Suy ra \(\Delta EIB=\Delta FIB\left(g.c.g\right)\).
Vì vậy IE = IF.
Chứng minh tương tự ta có ID = IF.
vì vậy ID = IE.

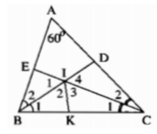
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
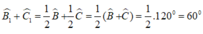
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID