Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác BAD cân nên ˆBDA=ˆBAD=700BDA^=BAD^=700. Từ đó ˆDAC=300DAC^=300
Tương tự ta tính được ˆBAE=300BAE^=300
Vậy ˆDAE=40

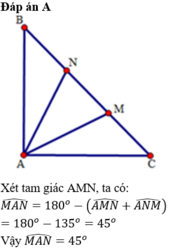
Tam giác BAM cân tại B ( BM=BA ); tam giác CAN cân tại C => Góc AMN = (180 độ - B):2; Góc ANM = (180-C):2
Góc AMN + Góc CAN = (360-(B+C))/2=(360-90)/2=135
Xét tam giác AMN có góc MAN = 180 - ( Góc AMN + Góc CAN) = 180 -135 =45
Chúc bạn học giỏi ;)

Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)

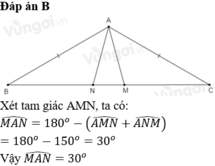
Xét ΔBAM có BM=BA(gt)
nên ΔBAM cân tại B(Định nghĩa tam giác cân)
hay \(\widehat{BAM}=\widehat{BMA}\)(hai góc ở đáy)
Xét ΔCAN có CA=CN(gt)
nên ΔCAN cân tại C(Định nghĩa tam giác cân)
hay \(\widehat{CNA}=\widehat{CAN}\)(hai góc ở đáy)
Ta có: \(\widehat{BAM}=\widehat{BMA}\)(cmt)
\(\widehat{CNA}=\widehat{CAN}\)(cmt)
Do đó: \(\widehat{BMA}+\widehat{CNA}=\widehat{BAM}+\widehat{CAN}\)
\(\Leftrightarrow\widehat{NMA}+\widehat{ANM}=110^0+\widehat{NAM}\)
Xét ΔNAM có
\(\widehat{NAM}+\widehat{ANM}+\widehat{AMN}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow110^0+\widehat{NAM}+\widehat{NAM}=180^0\)
\(\Leftrightarrow2\cdot\widehat{NAM}=70^0\)
hay \(\widehat{MAN}=35^0\)
Vậy: \(\widehat{MAN}=35^0\)