Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GỌi E;F thứ tự là hình chiếu của B,C trên AM và S1;S2;S3 là diện tích các tam giác AMB;AMC;BMC Ta có:
AM.BE+AM.CFAM.BE+AM.CF \leq AM.BD+AM.CDAM.BD+AM.CD Hay 2S1+2S22S1+2S2 \leq AM.(BD+CD)=AM.BC
Dấu = xảy ra khi AM vuông góc BC
tương tự có: 2S1+2S32S1+2S3 \leq BM.AC
2S2+2S32S2+2S3 \leq CM.AB
\Rightarrow AM.BC+BM.AC+CM.AB \geq 4SABC4SABC
dấu = xảy ra khi M là trực tâm tam giác ABC
D là giao điểm của AM và BC
chúc bạn học tốt
ĐÚNG 100%

Ta dựng các tam giác đều AMP , AMN , ACE , ABD , suy ra N,P,E,D cố định.
Dễ dàng chứng minh được \(\Delta APE=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow MC=PE\), \(AM=MP\)
Suy ra : \(AM+MC+BM=BM+MP+PE\ge BE\)(hằng số)
Tương tự , ta cũng chứng minh được \(AM=MN\), \(BM=DN\)
\(\Rightarrow AM+MC+MB=CM+MN+DN\ge CD\)(hằng số)
Suy ra MA + MB + MC đạt giá trị nhỏ nhất khi M là giao điểm của BE và CD.
Cần chú ý : Vì điều kiện các góc của tam giác nhỏ hơn 180 độ :
\(\widehat{BAC}+\widehat{CAE}< 120^o+60^o=180\)
\(\widehat{BAC}+\widehat{BAD}< 120^o+60^o=180^o\)
nên BE cắt AC tại một điểm nằm giữa A và C , CD cắt AB tại một điểm nằm giữa A và B. Do đó tồn tại giao điểm M của CD và BE.

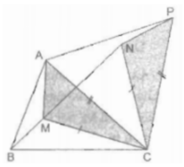
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
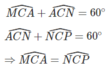
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
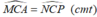
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.


Vẽ các đường kính AM, BN, CP của (O). Dễ cm được BMCH, CNAH,APBH là các hình bình hành => AH = CN; BH = CM; CH = BM
=> AH + BH + CH = CN + CM + BM
Vì BC cố định nên CN không đổi => (AH + BH + CH) max khi (CM + BM) max. Ta sẽ cm rằng điều đó xảy ra khi M trùng điểm chính giữa cung nhỏ BC.
Thật vậy gọi Q là điểm chính giữa cung nhỏ BC. Kéo dài BQ đoạn QD = BQ = CQ, kéo dài BM đoạn ME = MC => BD = BQ + CQ = 2BQ và BE = BM + CM
Vì tg CQD cân tại Q => ^BDC = ^QCD = ^BQC/2
Tương tự tg CME cân tại M => ^BEC = ^MCE = ^BMC/2
Mà ^BMC = ^BQC => ^BEC = ^BDC => B,C,D,E cùng thuộc đường tròn đường kính BD => BE =< BD <=> BM + CM =< 2BQ => (BM + CM)
Max = 2BQ xảy ra khi E trùng D hay khi M trùng Q khi đó A là điểm chính giữa cung lớn BC
bài nay f trong sách nâng cao chuyên đề hình học 8 phần cực trị nhé
bạn gi ra dùm mk với mình ko có sách đó.