Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ A dựng đường thẳng vuông góc với BC căt BC tại M
Xét tg vuông ABM và tg vuông BDH có
\(BD\perp BA;HB\perp AM\Rightarrow\widehat{HBD}=\widehat{MAB}\) (góc có cạnh tương ứng vuông góc)
\(BD=BA\left(gt\right)\)
\(\Rightarrow\Delta BDH=\Delta ABM\) (hai tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau)
\(\Rightarrow DH=BM\)
Chứng minh tương tự ta cũng có \(EK=CM\)
\(\Rightarrow DH+EK=BM+CM=BC\left(đpcm\right)\)

A B C D H K E F
Kẻ đường cao AF.
Vì BD \(\perp\) BA nên \(\widehat{DBA}\) = 90o
Ta có: \(\widehat{DBH}\) + \(\widehat{DBA}\) + \(\widehat{ABF}\) = 180o
=> \(\widehat{DBH}\) + \(\widehat{ABF}\) = 90o (1)
Áp dụng tính chất tam giác vuông ta có:
\(\widehat{ABF}\) + \(\widehat{BAF}\) = 90o (2)
Từ (1) và (2) suy ra:
\(\widehat{DBH}\) + \(\widehat{ABF}\) = \(\widehat{ABF}\) + \(\widehat{BAF}\)
=> \(\widehat{DBH}\) = \(\widehat{BAF}\)
Xét \(\Delta\)BHD vuông tại H và \(\Delta\)AFB vuông tại F có:
BD = AB (gt)
\(\widehat{DBH}\) = \(\widehat{BAF}\) (c/m trên)
=> \(\Delta\)BHD = \(\Delta\)AFB (ch - gn)
=> DH = BF (2 cạnh t/ư) (3)
Chứng minh tương tự:
\(\Delta\)EKC = \(\Delta\)CFA (ch - gn)
=> EK = CF (2 cạnh t/ư) (4)
Ta có: BF + CF = BC (5)
Thay (3); (4) vào (5) ta được:
DH + EK = BC \(\rightarrow\) đpcm

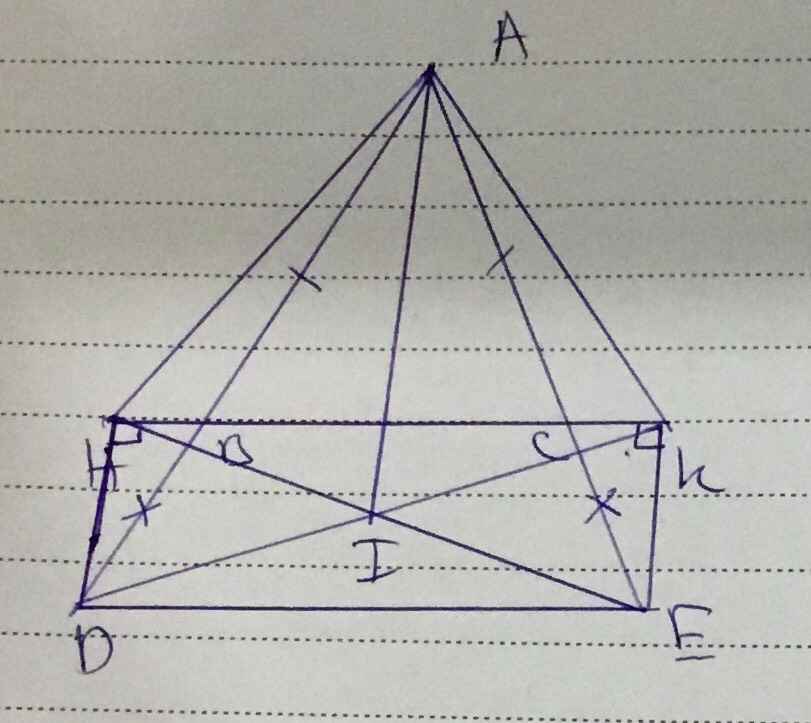
Cho tam giác ABC có góc B và góc C nhọn, AB < AC, đường cao AH. Vẽ đường thẳng BD = BA, BD vuông góc với BA sao cho C và D khác phía đối với AB. Vẽ đoạn thẳng CE = CA , CE vuông góc với CA sao cho B và E khác phía đối với AC. Kẻ DI vuông góc với BC tại I và EK vuông góc với BC tại K. Chứng minh : 1) góc ABH phụ với góc DBI 2) góc ABH = góc BDI và góc BAH = góc DBI 3) tam giác ABH = tam giác DBI 4) tam giác ACH = tam giác CEK 5) BI = CK
trình bày bài này lâu lém
tự vận dụng kiến thức mà làm
suy nghĩ đi
động não đi

DH song song EK9 vì cung vuông góc BC)
HDM = MEK (S.L.T)
xét tam giác BDH và tam giác CEK
góc B = KCE vì cùng = góc C
BD = CE
Suy ra 2 tam giác này = nhau theo TH (ch-gn)
Suy ra DH = KE
xét tam giác DHM và tam giác EKM
DH = KE
HDM = MEK (cmt)
Suy ra 2 tam giác này = nhau theo TH (g-c-g)
Suy ra HMD = EMK
HMD+DMK=180 2 góc kề bù
Suy ra EMK+DMK=180
Suy ra D,M,E thẳng hàng
bạn Long vu lm sai r bn từ dh song song với ke mà suy ra hai góc đs bằng nhau thì chẳng khác j ns c, m, e thẳng hàng cả