

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



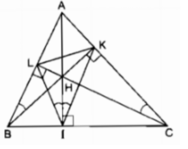
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác BIHL nội tiếp.

Tứ giác CIHK nội tiếp.

Từ (1), (2) suy ra:

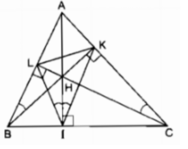
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có ![]()
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có ![]()
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có ![]()
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có ![]()
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có ![]()
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có 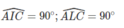
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.

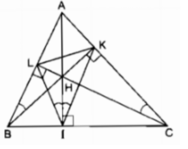
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.



Bài 1:
b)
chứng minh EDCB là tgnt => góc AED = góc ACB
từ đó, chứng minh tam giác AED đồng dạng ACB (gg)
=> DE / BC = AD / AB
tam giác ADB vuông tại A => AD / AB = cotg A = cotg 45 = 1
c)
kẻ tiếp tuyến tại Ax của (O) (Ax thuộc nửa mp bờ AC chứa B)
góc xAB = ACB = AED
=> DE // Ax
Mà Ax vuông góc với OA nên OA vuông góc với DE. (đpcm)

A B C O M N E K T
a) Có ^AOB = 1800 - ^OAB - ^OBA = 1800 - ^BAC/2 - ^ABC/2 = 900 + (1800 - ^BAC - ^ABC)/2 = 900 + ^ACB/2
b) Dễ thấy A,M,O,E cùng thuộc đường tròn đường kính OA (Vì ^AMO = ^AEO = 900) (1)
Ta có ^AOK = 1800 - ^AOB = 1800 - (900 + ^ABC/2) = 900 - ^ACB/2 = ^CEN (Do \(\Delta\)CEN cân tại C)
=> Tứ giác AOKE nội tiếp hay A,O,K,E cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra năm điểm A,M,K,O,E cùng thuộc một đường tròn (đpcm).
c) Ta thấy A,O,K,E cùng thuộc một đường tròn (cmt) và OK cắt AE tại T
Nên \(\frac{KT}{ET}=\frac{AT}{OT}\)(Hệ thức lượng đường tròn). Kết hợp \(\frac{AT}{OT}=\frac{AB}{OB}\)(AO là phân giác ^BAT)
Suy ra \(\frac{KT}{ET}=\frac{AB}{OB}\). Mặt khác: ^BKN = ^OAE = ^BAO và ^NBK = ^OBA => \(\Delta\)BKN ~ \(\Delta\)BAO (g.g)
=> \(\frac{AB}{OB}=\frac{KB}{NB}\). Từ đây \(\frac{KT}{ET}=\frac{KB}{BN}\)=> KT.BN = KB.ET (đpcm).

a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành

J A B C O E D H K M N
a) Xét hai tam giác ABD và ACE có:
\(\widehat{A}\) chung
\(\widehat{ADB}=\widehat{AEC}=90^o\)
\(\Rightarrow\Delta ABD\sim\Delta ACE\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AC}=\frac{AD}{AE}\Rightarrow AD.AC=AE.AB\)
b) Xét tam giác ABC có BD và CE là hai đường cao nên H là trực tâm. Vậy thì AH vuông góc với BC tại K.
c) Ta thấy AMO; AKO; ANO là các tam giác vuông có chung cạnh huyền AO nên A, M, K, O, N cùng thuộc đường tròn đường kính AO.
Khi đó \(\widehat{AKN}=\widehat{AMN}\) (Hai góc nội tiếp cùng chắn cung AN)
Lại có AM = AN nên \(\widehat{AMN}=\widehat{ANM}\)
Suy ra \(\widehat{AKN}=\widehat{ANM}\)
d) Gọi J là giao điểm của MN với AO.
Xét tam giác vuông ANO, đường cao NJ, ta có:
\(AJ.AO=AN^2\) (Hệ thức lượng)
Lại có \(\Delta AHJ\sim\Delta AOK\left(g-g\right)\Rightarrow\frac{AH}{AO}=\frac{AJ}{AK}\)
\(\Rightarrow AJ.AO=AH.AK\)
\(\Rightarrow AN^2=AH.AK\)
\(\Rightarrow\Delta AHN\sim\Delta ANK\left(c-g-c\right)\Rightarrow\widehat{ANH}=\widehat{AKN}\)
Mà \(\widehat{AKN}=\widehat{ANM}\Rightarrow\widehat{ANH}=\widehat{ANM}\) hay M, N, H thẳng hàng.
Hoàng Thị Thu Huyền ơi ngộ nhận kìa. ý d đang chứng minh thẳng hàng mà bạn có 2 cái tam giác AHJ và AOK đồng dạng (g g) thì sao được ??