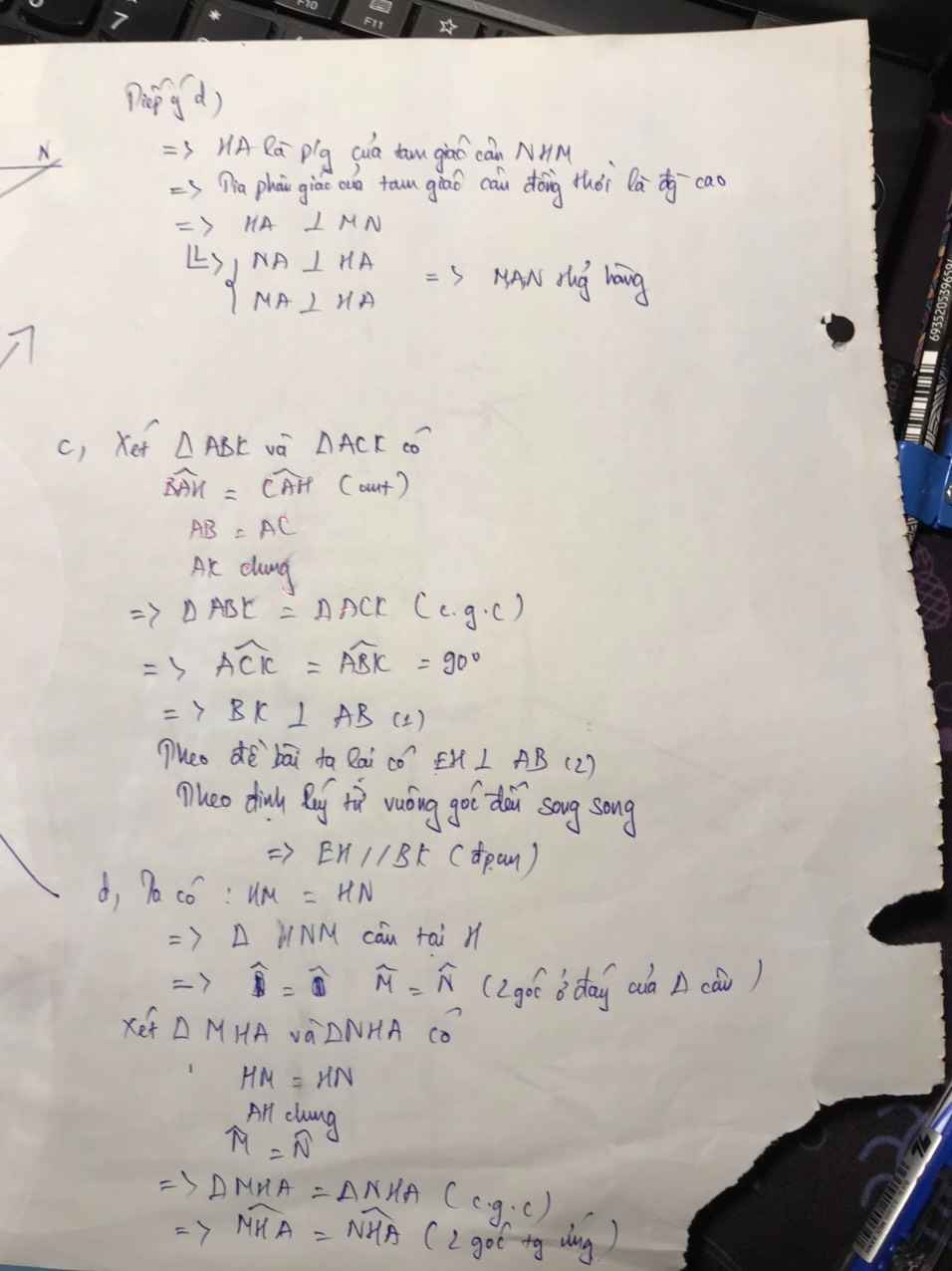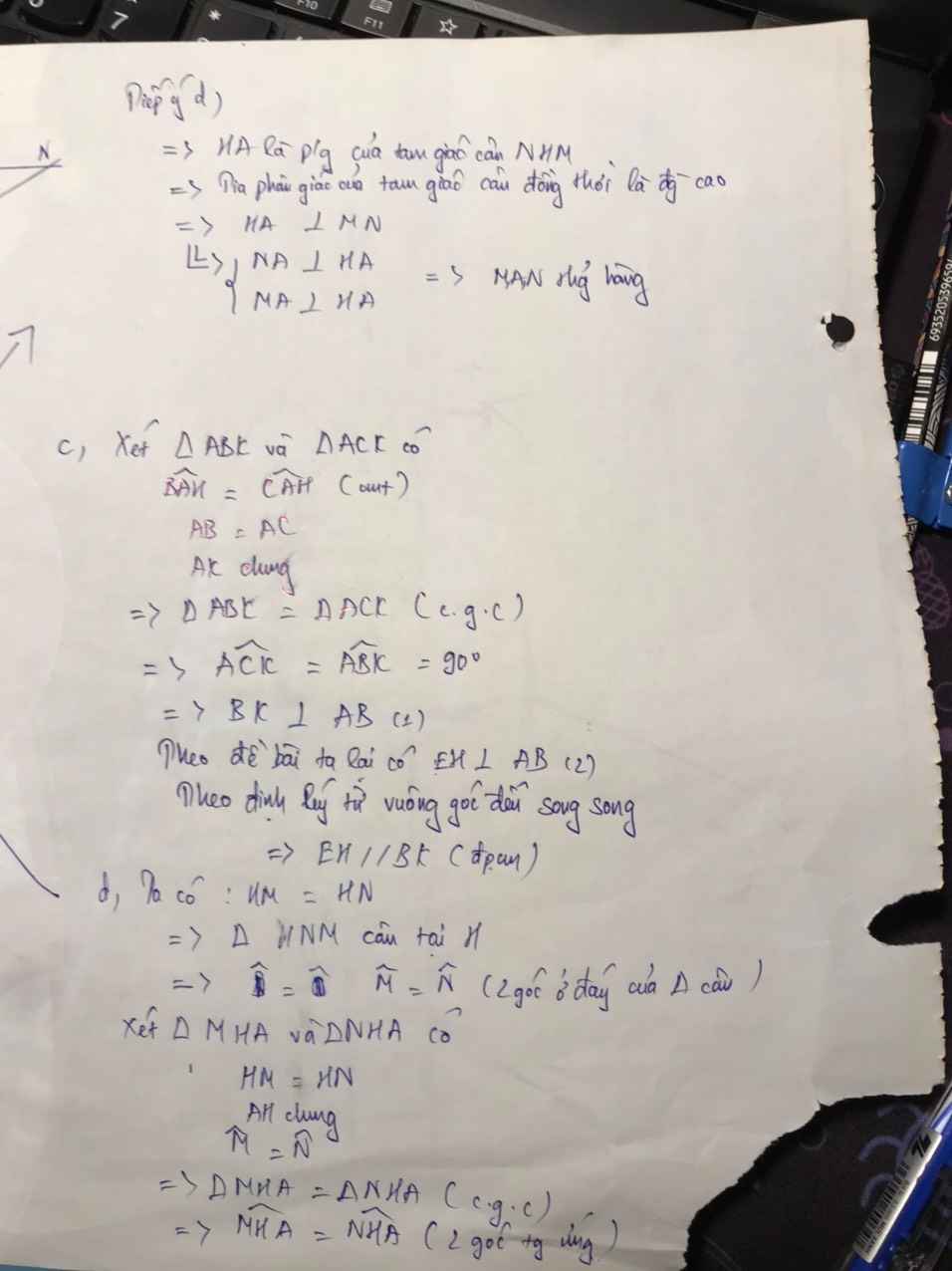Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔMHC và ΔMKC có
CH=CK
\(\widehat{HCM}=\widehat{KCM}\)
CM chung
Do đó: ΔMHC=ΔMKC
Suy ra: MH=MK
a ) Vì CM là tia phân giác của góc KCH
\(\Rightarrow\)Góc KCM = Góc HCM = 50° / 2 = 25°
Trong \(\Delta\)CHM có :
Góc MHC + Góc CMH + Góc MCH = 180°
\(\Leftrightarrow\)90° + Góc CMH + 25° = 180°
\(\Leftrightarrow\)Góc CMH = 65°
b ) Xét \(\Delta\)CMK và \(\Delta\)CMH có :
- CK = CH ( giả thiết )
- Góc KCM = Góc HCM ( vì CM là tia phân giác của góc KCH )
- MC : cạnh chung
\(\Rightarrow\)\(\Delta\)CMK = \(\Delta\)CMH ( C - G - C )
\(\Rightarrow\)MK = MH ( 2 cạnh tương ứng )
c ) Ta có : MK = MH ( cmt )
\(\Rightarrow\)M nằm trên đường trung trực của KH ( 1 )
Ta lại có : CK = CH ( giả thiết )
\(\Rightarrow\)C nằm trên đường trung trực của KH ( 2 )
Từ ( 1 ) và ( 2 ), suy ra MC là đường trung trực của KH
\(\Rightarrow\)MC \(\perp\)KH
d ) Ta có : Góc KCH + Góc HCN = 90° ( vì NC \(\perp\)KC )
\(\Rightarrow\)Góc KCM + Góc HCM + Góc HCN = 90°
\(\Rightarrow\)25° + Góc NCM = 90°
\(\Rightarrow\)Góc NCM = 65°
Mà ta có : Góc NMC = 65°
\(\Rightarrow\)Góc NCM = Góc NMC
