Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải chi tiết:
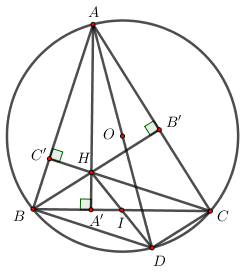
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.
Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH
Chứng minh tương tự ta có CD∥BHCD∥BH.
⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.
c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.
Ta có:
SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′
Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC
⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2

A B C A' B' C' Hình vẽ chỉ mang tính chất minh họa
Ta có : \(\frac{AH}{AA'}=\frac{S_{ABH}}{S_{ABA'}}=\frac{S_{ACH}}{S_{ACA'}}=\frac{S_{ABH}+S_{ACH}}{S_{ABC}}\) ( Tính chất dãy tỉ số bằng nhau, tỉ số diện tích )
Tương tự ta có :
\(\frac{BH}{BB'}=\frac{S_{AHB}+S_{BHC}}{S_{ABC}}\) , \(\frac{CH}{CC'}=\frac{S_{ACH}+S_{BHC}}{S_{SBC}}\)
Do đó :
\(\frac{AH}{AA'}+\frac{BH}{BB'}+\frac{CH}{CC'}=\frac{2\left(S_{ABH}+S_{AHC}+S_{BHC}\right)}{S_{ABC}}=\frac{2\cdot S_{ABC}}{S_{ABC}}=2\)
Vậy : \(\frac{AH}{AA'}+\frac{BH}{BB'}+\frac{CH}{CC'}=2\)

Ta có: = 2
= 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và =
(đối đỉnh)
mà = 180o -
= 180o - 60o = 120o
nên = 120o (2)
=
+
= 60o + = 60o+ 60o
(sử dụng góc ngoài của tam giác)
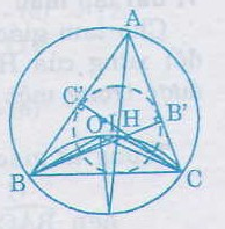
Do đó = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)
mà \(\widehat{B'HC'}\) = 180o - \(\widehat{A}\) = 180o - 60o = 120o
nên \(\widehat{BHC}\) = 120o (2)
\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)
= 60o + \(\dfrac{180^0-60^0}{2}\) = 60o+ 60o
(sử dụng góc ngoài của tam giác)

Do đó \(\widehat{BIC}\) = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn

A B C O I A' B' C' E F D G S
a) Ta có ^AIC' = ^IAC + ^ICA = ^IAB + ^ICB = ^IAB + ^BAC' = ^IAC' => \(\Delta\)AC'I cân tại C'
=> C' nằm trên trung trực của AI. Tương tự B' cũng nằm trên trung trực của AI => B'C' vuông góc AI
Hay A'I vuông góc với B'C'. Lập luận tương tự B'I vuông góc A'C', C'I vuông góc A'B'
Do đó I là trực tâm của \(\Delta\)A'B'C' (đpcm).
b) Ta thấy ^FDE = ^A'DC' = ^A'AC' = ^IAC' = C'IA (Vì \(\Delta\)AC'I cân tại C') = ^EIC'
Suy ra tứ giác DEIF nội tiếp (đpcm).
c) Gọi S là tâm ngoại tiếp của \(\Delta\)DEF. Vì tứ giác DEIF nội tiếp (cmt) nên S đồng thời là tâm ngoại tiếp DEIF
Gọi giao điểm thứ hai giữa (S) và (O) là G. Khi đó ^DFG = ^DEG => ^GFA' = ^GEC'
Lại có ^EGF = ^EDF = ^A'DC' = ^A'GC' => ^FGA' = ^EGC'. Do vậy \(\Delta\)GEC' ~ \(\Delta\)GFA' (g.g)
=> \(\frac{GC'}{GA'}=\frac{EC'}{FA'}\). Mặt khác ^A'IF = ^C'IA = ^C'AI = ^C'AE và ^IA'F = ^AA'D = ^AC'D = ^AC'E
Cho nên \(\Delta\)AEC' ~ \(\Delta\)IFA' (g.g) => \(\frac{EC'}{FA'}=\frac{AC'}{IA'}\). Mà các điểm A,I,A',C' đều cố định
Nên tỉ số \(\frac{AC'}{FA'}\) là bất biến. Như vậy \(\frac{GC'}{GA'}\)không đổi, khi đó tỉ số giữa (GC' và (GA' của (O) không đổi
Kết hợp với (O), A',C' cố định suy ra G là điểm cố định. Theo đó trung trực của IG cố định
Mà S thuộc trung trực của IG (do D,I,E,F,G cùng thuộc (S)) nên S di động trên trung trực của IG cố định (đpcm).