Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

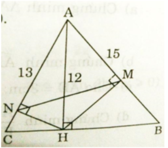
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
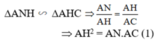
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
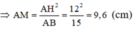
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()

Tam giác AHN đồng dạng với tam giác ACH ( tự chứng minh )
\(\Rightarrow\frac{AH}{AC}=\frac{AN}{AH}\Rightarrow AH^2=AN.AC\left(1\right)\)
tam giác AHB đồng dạng với tam giác AMH ( Tự chứng minh )
\(\Rightarrow\frac{AH}{AM}=\frac{AB}{AH}\Rightarrow AH^2=AB.AM\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra AB.AM = AN.AC
\(\Rightarrow\frac{AC}{AB}=\frac{AM}{AN}\)
Xét tam giác AMN và tam giác ACB có:
\(\widehat{MAN}\)chung
\(\frac{AM}{AN}=\frac{AC}{AB}\left(cmt\right)\)
Suy ra tam giác AMN đồng dạng với tam giác ACB ( c-g-c )
b) Áp dụng định lý PITAGO tính ra BH và CH
rồi tiếp tục tính tiếp BC
- bạn ơi
- Chứng minh ngay luôn hộ mình để mình còn gửi bài cho cô nè. mình không có time đâu bạn

A ) ÁP DỤNG ĐỊNH LÍ PITAGO TA CÓ :
\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(15^2-12^2=81\)
\(\Rightarrow BH=\sqrt{81}=9\)(cm)
Ap dụng pitago ta lại có :
\(HC^2=AC^2-AH^2\)
\(\Leftrightarrow HC^2=13^2-12^2=25\left(CM\right)\)
\(\Rightarrow HC=\sqrt{25}=5\left(cm\right)\)
Vậy : \(BC=BH+HC=5+9=14\left(cm\right)\)
sao lại sử dụng Py - ta - go đc ? tam giác ABC nhọn mà

B H M A C N
( Hình ảnh chỉ mang tính chất minh họa )
a) Tính BC và AH :
Tam giác ABC vuông tại A, áp dụng định lý Pytago vào tam giác ABC :
AB2+AC2=BC2AB2+AC2=BC2
82+152=BC282+152=BC2
⇒BC=17(cm)⇒BC=17(cm)
Ta có : SABC=12⋅AB⋅AC=12⋅AH⋅BCSABC=12⋅AB⋅AC=12⋅AH⋅BC
⇔AH=AB⋅ACBC=8⋅1517=12017(cm)⇔AH=AB⋅ACBC=8⋅1517=12017(cm)
b) Có Aˆ=900A^=900(giả thiết),

Bài làm
a) Vì AH vuông góc với BC
=> Tam giác AHC vuông ở H.
=> \(\widehat{HAC}+\widehat{C}=90^0\) (1)
Vì HN vuông góc với AC
=> Tam giác HNC vuông ở N
=> \(\widehat{NHC}+\widehat{C}=90^0\) (2)
Từ (1) và (2) => \(\widehat{HAC}=\widehat{NHC}\)
Xét tam giác AHN và tam giác ACH có:
\(\widehat{ANH}=\widehat{HNC}\left(=90^0\right)\)
\(\widehat{HAC}=\widehat{NHC}\)
=> Tam giác AHN ~ tam giác ACH ( g - g )
b) Xét tam giác AHB vuông ở H,
Theo định lí Thales có:
\(AB^2=AH^2+HB^2\)
Hay \(15^2=12^2+HB^2\)
\(\Rightarrow225=144+HB^2\)
\(\Rightarrow HB^2=81\)
\(\Rightarrow HB=9\left(cm\right)\)
Xét tam giác AHC vuông ở H có:
\(AC^2=AH^2+HC^2\)
hay \(13^2=12^2+HC^2\)
\(\Rightarrow169=144+HC^2\)
\(\Rightarrow HC^2=25\left(cm\right)\)
\(\Rightarrow HC=5\left(cm\right)\)
Ta có: HB + HC = BC
hay 9 + 5 = BC
=> BC = 14 ( cm )


a: ΔAHB vuông tại H
mà HN là đường cao
nên AN*AB=AH^2
ΔAHC vuông tại H
mà HM là đường cao
nên AM*AC=AH^2
=>AN*AB=AM*AC
=>AN/AC=AM/AB
=>ΔANM đồng dạng với ΔACB
b: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(CH=\sqrt{13^2-12^2}=5\left(cm\right)\)
=>BC=14cm