Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì MD là trung trực AB trong ∆AMD
=> ∆AMD cân tại A
=> AM = AD
Vì DN là trung trực AC trong ∆ADN
=>∆ADN cân tại A
=> AD = AN
Mà AM = AD
=> AM = AN
=> ∆AMN cân tại A

tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))
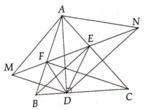


Hình vẽ: (Bạn nên tự vẽ hình theo mô tả để dễ theo dõi)
Phân tích ban đầu:
a) Chứng minh △AMN cân tại A (Lưu ý: Đề bài yêu cầu C/m △ABC cân tại A là không chính xác vì giả thiết cho AB < AC)
(Ghi chú: Không thể chứng minh △ABC cân tại A vì điều đó mâu thuẫn với giả thiết AB < AC. Rất có thể đề bài có sự nhầm lẫn ở câu a và ý đúng là chứng minh △AMN cân tại A)
b) Chứng minh DA là tia phân giác của góc EDF
Để chứng minh DA là tia phân giác của góc EDF, ta cần chứng minh ∠ADE = ∠ADF.
c) Chứng minh ba đường thẳng AD, BE, CF đồng quy
Ta sẽ sử dụng định lý Ceva dạng sin trong tam giác ABC đối với các đường thẳng AD, BE, CF. Ba đường thẳng này đồng quy khi và chỉ khi:
(sin ∠BAD / sin ∠DAC) * (sin ∠ACF / sin ∠BCF) * (sin ∠CBE / sin ∠ABE) = 1 (*)
(sin ∠BAD / sin ∠DAC) * [(AF/BF) * (sin(A)/sin(B))] * [(CE/AE) * (sin(C)/sin(A))] = 1
(sin ∠BAD / sin ∠DAC) * (AF/BF) * (CE/AE) * (sin C / sin B) = 1
(sin ∠BAD / sin ∠DAC) * (AC/BC) * (BC/AB) * (sin C / sin B) = 1
(sin ∠BAD / sin ∠DAC) * (AC/AB) * (sin C / sin B) = 1
(sin ∠BAD / sin ∠DAC) * (sin B / sin C) * (sin C / sin B) = 1
sin ∠BAD / sin ∠DAC = 1
sin ∠BAD = sin ∠DAC
∠BAD = ∠DAC
Nếu đề bài cho tam giác ABC cân tại A (AB=AC) thì AD, BE, CF sẽ đồng quy. Có thể đề bài gốc có giả thiết là △ABC cân tại A hoặc có một yêu cầu khác trong phần c). Dựa trên giả thiết AB < AC, kết luận là chúng không đồng quy.
a: Sửa đề: Chứng minh ΔAMN cân tại A
Ta có: AB là đường trung trực của DM
=>AM=AD và BD=BM
ta có: AC là đường trung trực của DN
=>AD=AN và CD=CN
Ta có: AM=AD
AN=AD
Do đó: AM=AN
=>ΔAMN cân tại A
b: Xét ΔAMB và ΔADB có
AM=AD
BM=BD
AB chung
Do đó: ΔAMB=ΔADB
=>\(\widehat{MAB}=\widehat{DAB};\widehat{MBD}=\widehat{DBA}\)
Xét ΔADC và ΔANC có
AD=AN
DC=NC
AC chung
Do đó:ΔADC=ΔANC
=>\(\widehat{DAC}=\widehat{NAC};\widehat{ACD}=\widehat{ACN}\)
Xét ΔAMF và ΔADF có
AM=AD
\(\widehat{MAF}=\widehat{DAF}\)
AF chung
Do đó: ΔAMF=ΔADF
=>\(\widehat{ADF}=\widehat{AMF}=\widehat{AMN}\left(1\right)\)
Xét ΔADE và ΔANE có
AD=AN
\(\widehat{DAE}=\widehat{NAE}\)
AE chung
DO đó: ΔADE=ΔANE
=>\(\widehat{ADE}=\widehat{ANE}=\widehat{ANM}\left(2\right)\)
ΔAMN cân tại A
=>\(\widehat{AMN}=\widehat{ANM}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{ADF}=\widehat{ADE}\)
=>DA là phân giác của góc FDE