Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hai góc này không bằng nhau thì chứng minh làm sao được em?
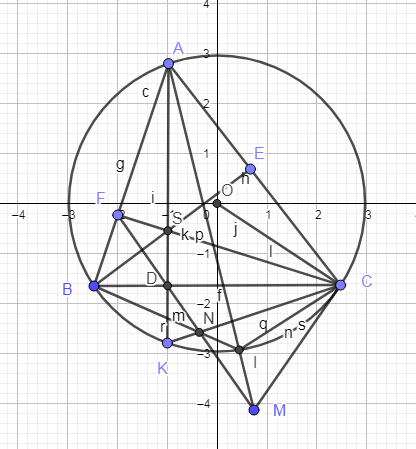
Em thử sử dụng tính năng đo góc của geogebra là biết.
ta có: \(MC^2=MI.MA\)
\(\Rightarrow MD^2=MI.MA\) ( do tam giác MCD cân tại M)
\(\Rightarrow\dfrac{MD}{MA}=\dfrac{ MI}{MD}\)
Xét tam giác MDI và tam giác MAD có :
\(\left\{{}\begin{matrix}DMAgócchung\\\dfrac{MD}{MA}=\dfrac{MI}{MD}\end{matrix}\right.\)
=> tam giác MDI đồng dạng tam giác MAD ( g -c)
=> góc MDI = góc MAD (1)
tứ giác DNIC nội tiếp => góc MDI = góc MCI (2)
từ 1 và 2 suy ra :góc NCI = góc HAD
mà góc MAD = góc KCI
=> góc NCI = góc KCI
vậy 3 điểm C ; K ; N thẳng hàng ( đpcm)
ACDF nội tiếp nên \(\widehat{BAC}+\widehat{CDF}=180^0\Rightarrow\widehat{BAC}=\widehat{CDN}\)
ABIC hiển nhiên nội tiếp \(\Rightarrow\widehat{BAC}+\widehat{NIC}=180^0\)
\(\Rightarrow\widehat{CDN}+\widehat{NIC}=180^0\Rightarrow CDNI\) nội tiếp
\(\Rightarrow\widehat{NDI}=\widehat{NCI}\) (cùng chắn IN)
MCD cân \(\Rightarrow MC=MD\Rightarrow MD^2=MC^2=MI.MA\Rightarrow\dfrac{MD}{MA}=\dfrac{MI}{MD}\) và \(\widehat{NMI}\) chung
\(\Rightarrow\Delta MDI\sim\Delta MAD\left(c.g.c\right)\)
\(\Rightarrow\widehat{NDI}=\widehat{MAD}\Rightarrow\widehat{MAD}=\widehat{NCI}\)
Mà \(\widehat{MAD}=\widehat{KCI}\) (cùng chắn cung IK)
\(\Rightarrow\widehat{KCI}=\widehat{NCI}\) hay K, N, C thẳng hàng
Đây chắc là 1 câu trong 1 bài nào đó, ít nhất em cũng phải nêu những câu trước có gì để người khác đỡ phải chứng minh từ đầu chứ?
MC^2=MI*MA=MD^2
=>MD/MA=MI/MD
=>ΔMDI đồng dạng với ΔMAD
DNIC nội tiếp
=>góc NDI=góc NCI
=>góc MCI=góc NAD
=>góc NCI=góc KCI
=>C,K,N thẳng hàng
ta có: MC2=MI.MA
⇒MD=MC ⇒MD2=MI.MA ( do tam giác MCD cân tại M)
⇒MD/ MA= MI/MD
Xét tam giác MDI và tam giác MAD có :
Góc M chung; MD/ MA= MI/MD
=> tam giác MDI đồng dạng tam giác MAD (c- g -c)
=> góc MDI = góc MAD (1)
tứ giác DNIC nội tiếp => góc MDI = góc MCI (2)
từ (1) và (2) suy ra :góc NCI = góc HAD
mà góc MAD = góc KCI
=> góc NCI = góc KCI
vậy 3 điểm C ; K ; N thẳng hàng ( đpcm)
có cả trường hợp NCI =KCI mà 3 điểm không thẳng hàng nữa mà?(N đối xứng với K)
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC