Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

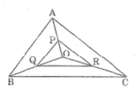
-Xét △OAB có: P trung điểm OA, Q trung điểm OB (gt)
\(\Rightarrow\)PQ là đường trung bình của △OAB.
\(\Rightarrow\)PQ=\(\dfrac{1}{2}\)AB.
\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
-Xét △OAC có: P trung điểm OA, R trung điểm OC (gt)
\(\Rightarrow\)PR là đường trung bình của △OAC.
\(\Rightarrow\)PR=\(\dfrac{1}{2}\)AC.
\(\Rightarrow\dfrac{PR}{AC}=\dfrac{\dfrac{1}{2}AC}{AC}=\dfrac{1}{2}\)
-Xét △OBC có: R trung điểm OC, Q trung điểm OB (gt)
\(\Rightarrow\)RQ là đường trung bình của △OBC.
\(\Rightarrow\)RQ=\(\dfrac{1}{2}\)BC.
\(\Rightarrow\dfrac{RQ}{BC}=\dfrac{\dfrac{1}{2}BC}{BC}=\dfrac{1}{2}\)
-Xét △PQR và △ABC có: \(\dfrac{PQ}{AB}=\dfrac{PR}{AC}=\dfrac{QR}{BC}\left(=\dfrac{1}{2}\right)\)
\(\Rightarrow\)△PQR ∼ △ABC (c-c-c)

Trong △ OAB, ta có PQ là đường trung bình nên: PQ =1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 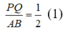 (1)
(1)
Trong △ OAC, ta có PR là đường trung bình nên:
PR = 1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 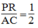 (2)
(2)
Trong △ OBC, ta có QR là đường trung bình nên
QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 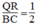
Từ (1), (2) và (3) suy ra: 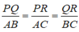
Vậy △ PQR đồng dạng △ ABC (c.c.c)

Cho tứ giác ABCD có 2 đường chéo AC và BD bằng nhau và cắt nhau tại O sao cho OC > OD. Gọi F, E, P, Q theo thứ tự là trung điểm AB, BC, CD, AD. Gọi Ot là phân giác góc DOC. Chứng minh rằng: Ot vuông góc QE.
Các bạn giúp mình với.. Mình sắp nộp bài rồi. Giải cụ thể nhé. Camon.
Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều
Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều

1: Xét ΔBCA có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔBCA
Suy ra: \(ED=\dfrac{BC}{2}=2\left(cm\right)\)